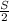м, тогда и вторая половина трассы будет иметь длину 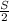м. Найдем час, за который автомобиль проехал первую половину трассы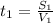 
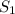- длинна первой половины трассы 
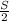м.
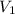- скорость на первой половине трассы 
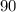км/ч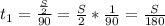
час за который автомобиль первую половину трассы.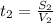
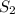-вторая половина трассы - 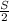м.
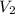- скорость на второй половине трассы 
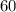км/ч.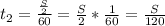
час за который автомобиль проехал вторую половину трассы.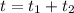
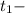
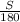
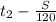
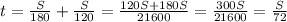
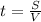
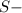длинна всей трассы, у нас получилась 
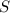м.
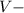скорость автомобиля на всей трассе, или средняя скорость.Получается что средняя скорость автомобиля на протяжении всего пути была 
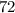км/ч.
собственно говоря, решается это всё методом замены переменной. Пусть x + y = a, xy = b. Выразим сумму квадратов во втором уравнении через a и b:
(x + y)² = x² + 2xy + y² или с учётом замены
a² = x² + y² + 2b, откуда
x² + y² = a² - 2b.Перепишем систему уже в другом виде:
a = 3 a = 3 a = 3
a² - 2b = 29 2b = a² - 29 = 9 - 29 = -20 b = -10
Теперь вернёмся к старым переменным x и y:
x + y = 3
xy = -10
Решаем эту систему обычным методом подстановки:
y = 3 - x
x(3-x) = -10 (1)
(1) -x² + 3x = -10
x² - 3x - 10 = 0
x1 = 5; x2 = -2
Таким образом, наша система распадается ещё на две:
x = 5 или x = -2
y = -2 y = 5
Раша система имеет две пары решений, что мы собственно и получили. Система решена.
0,1tz^2 * (t - 2z)(t^2 + 2tz + 4z^2)
То есть третий вариант ответа