Question

1.решить уравнение: 2cos^2x-sinx-1=0. 2.докажите,что функция у=(2х+5)^10 удовлетворяет соотношению 8000у(2х+5)^17-(у')^3=0. 3.найдите знаменатель бесконечно убывающей прогрессии,у которой каждый член в 6 раз больше суммы всех её
последующих членов.

Answer 1

$\tt 1.~~2\cos^2x-\sin x-1=0\\ 2(1-\sin^2x)-\sin x-1=0\\ 2-2\sin^2x-\sin x-1=0\\ 2\sin^2x+\sin x-1=0$

Решим это уравнение как квадратное уравнение относительно sinx

$\tt D=b^2-4ac=1^2-4\cdot2\cdot(-1)=1+8=9\\ \\ \sin x=\dfrac{-1+3}{2\cdot2}=0.5~~~\Rightarrow~~~ \boxed{\tt x=(-1)^k\cdot\frac{\pi}{6}+\pi k,k \in \mathbb{Z}} \\ \\ \sin x=\dfrac{-1-3}{2\cdot2}=-1~~~\Rightarrow~~~\boxed{\tt x=-\frac{\pi}{2}+2\pi k,k \in \mathbb{Z}}$

2. Производная функции: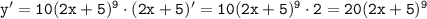 $\tt y'=10(2x+5)^9\cdot(2x+5)'=10(2x+5)^9\cdot2=20(2x+5)^9$

$\tt 8000y(2x+5)^{17}-(y')^3=8000(2x+5)^{10}(2x+5)^{17}-(20(2x+5)^{9})^3=\\ \\ =8000(2x+5)^{17}-8000(2x+5)^{27}=0$

Что и нужно было доказать.

3.

$\tt \frac{b_1}{q}$ - предыдущий член суммы последующих членов

$\tt S_1$ - сумма всех последующих членов г.п.

$\tt S$ - сумма бесконечно убывающей геом. прогрессии

$\tt S_1=6S~~~\Rightarrow~~~ \dfrac{b_1}{q} =6\cdot \dfrac{b_1}{1-q} \\ \\ 1-q=6q\\ \\ 7q=1\\ \\ q=\dfrac{1}{7}$

ответ: 1/7.