Послідовність задано формулою An=6-3л. Знайдіть під яким номером посдідовність містить число - 51

👇

Увидеть ответ

Открыть все ответы

Ответ:

stanislavovichs

03.05.2022

№1.

$\tt \displaystyle g(x)=\frac{x-5}{x+3}$

$\displaystyle g(-2)=\frac{-2-5}{-2+3} =\frac{-7}1 =-7\\ \\ g(2)=\frac{2-5}{2+3} =\frac{-3}{5} ^{(2}=\frac{-6}{10} =-0,\! 6$

№2.

$\tt \displaystyle f(x)=\frac1{-3x+2}$

$\displaystyle f(x)=1\Rightarrow \frac1{-3x+2}=1\; \; |\cdot (-3x+2)\ne 0\\ \\ \begin{Bmatrix}1=-3x+2\\ -3x+2\ne 0\end{matrix} \quad \begin{Bmatrix}3x=1\ne 2\\ 3x\ne 2\qquad \end{matrix} \\ \\ x=\frac13$

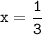
ответ: $\tt \displaystyle x=\frac13$

№3.

а)

f(x) = 19-2x; D(f) = (-∞;+∞)

б)

g(x) = x+1; D(g) = (-∞;+∞)

в)

y(x) = √x; D(y) = [0;+∞)

г)

y = x²-4; D(y) = (-∞;+∞)

Область определения линейных функций (пункты а и б) и квадратных (пункт г) ничто не ограничивает. А вот для квадратного корня есть ограничения - подкоренное выражение не может быть отрицательным (в пункте в) x ≥ 0).

№4.

а)

y = 37x+1; E(y)=(-∞;+∞)

б)

y = -23; E(y) = -23

в)

y = x; E(y) = (-∞;+∞)

г)

y = |x|; E(y) = [0;+∞)

Для линейной функция вида y=kx+b, k≠0, множество значений все действительные числа (пункты а и в). Для линейной функции вида y=b, b - константа, множество значений и есть число b, оно неизменно (пункт б). Множество значений модуля, все неотрицательные числа (пункт г).

ответы на вопросы:

1. Графиком квадратичной функции является парабола.

2. Привести функцию к виду f(x) = ax²+bx+c, абсцисса вершины: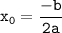 $\tt \displaystyle x_0 =\frac{-b}{2a}$ , ордината вершины: y₀ = f(x₀) - надо подставить значение x₀ в квадратичную функцию.

3. Направление ветвей зависит от старшего коэффициента.

Если a<0, то ветви направлены вниз;

Если a>0, то ветви направлены вверх.

4. Да, любая парабола имеет ось симметрии, для графика функции y=ax²+bx+c, ось симметрии будет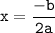 $\tt \displaystyle x =\frac{-b}{2a}$

5. Определяем координаты вершины парабола и направление ветвей. Если вершина ниже оси Ox, а ветви направлены вниз ИЛИ вершина выше оси Ox, а ветви направлены вверх, то искать нули функции (x, при которых график функции пересекает ось Ox) не надо. В остальных двух случаях, находим нули функции.

Составляем таблицу точек, для таких x, что не очень далеко от абсциссы вершины. И заодно находим координаты точки пересечения графика с осью Oy (x=0).

Отмечаем точки из таблицы и вершину на координатной плоскости и проводим параболы, подписываем координаты точек пересечения графика с ось Ox.

$Решите по , 9 класс. большое! ) номер 1. найдите g (-2) b g (2), если g (x)= x-5\x+3 номер 2. найдит$