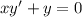
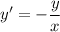 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными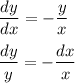
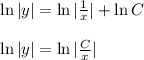
 - общее решение
- общее решение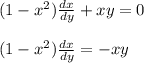

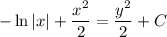 - общий интеграл
- общий интеграл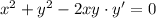

 , тогда
, тогда 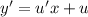



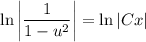
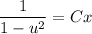
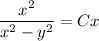 - общий интеграл
- общий интеграл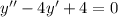
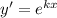 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
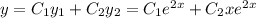 - общее решение
- общее решение
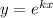 , тогда получаем
, тогда получаем
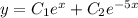

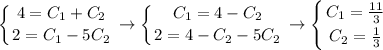
 - частное решение
- частное решение
Объяснение:
Найдите корни уравнений
1. 1) x²-5x-5=x-5;
x²-5x-x-5+5=0;
x²-6x=0;
x(x-6)=0;
x1=0;
x2=6.
***
2) -2x²+7x=3x ;
-2x²+7x-3x=0;
-2x²+4x=0;
-2x(x-4)=0;
x1=0;
x2=4.
***
3) 2-7x²+1,8x=2-3x;
2-7x²+1.8x-2+3x=0;
-7x²+4.8x=0;
-x(7x-4.8)=0;
x1=0;
7x=4.8;
x2=4.8/7 =48/70.
***
4) -2x²+5=5-4x;
-2x²+4x=0;
-2x(x-2)=0;
x1=0;
x2=2.
***
5) -0,8x²-9,2x=2,1x ;
-0.8x²-9.2x-2.1x=0;
-0.8x²-11.3x=0;
-0.8x(x+14.125)=0;
x1=0;
x2=-14.125.
***
6) 2-0,7x²+3x=x+2;
-0,7x² +3x-x=0;
-0.7x²+2x=0;
-x(0.7x-2)=0;
x1=0;
0.7x=2;
x=2/0.7=20/7=2 6/7.
***
2. 1) x²-5x=5(5-x) ;
x²-5x-25+5x=0;
x²-25=0;
x²=25;
x=±5.
***
2) -2x²+7x=7x-32 ;
-2x²+32=0;
-x²=-16;
x²=16;
x=±4.
***
3) -0,7x²+5,6x=0 ;
-0,7x(x-8)=0;
x1=0;
x2=8.
***
4) 2x²-x=2-x;
2x²=2;
x²=1;
x=±1.
***
5) -0,8x²-9,2=4,5;
-0.8x²=9.2+4.5;
-0.8x²= 13.7;
x²= -13.7/0.8;
x²= -17.125; (x² не может быть отрицательным. Нет решения).
***
6) -0,7x²+x=x ;
-0,7x²=0;
x=0.
Объяснение:
90°<а<180°; sina=✓3/3
90°<а<180°⇒cosa<0⇒cosa=-√(1-sin²a)=-√(1-(✓3/3)²)=-√(1-1/3)=-√(2/3)
tga=sina/cosa=(✓3/3)/(-√(2/3))=-√(3/2)
ctga=1/tga=1/(-√(3/2))=-√(2/3)