Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 6, 12, 14 и 8, тогда получим четыре числа, которые образуют арифметическую прогрессию. Найди числа, которые образуют геометрическую прогрессию.
знаменатель геометрической прогрессии: q= 2
члены геометрической прогрессии :
b1= 4
b2=8
b3= 16
b4=32
Решение
b₁; b₁·q; b₁·q²; b₁·q³ геометрическая прогрессия
тогда
b₁+6; b₁·q+12; b₁·q; b₁·q³ арифметическая прогрессия
по характеристическому свойству арифметической прогрессии
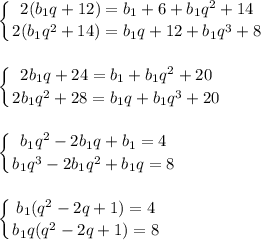
q ≠ 1
разделим второе уравнение на первое
q = 2
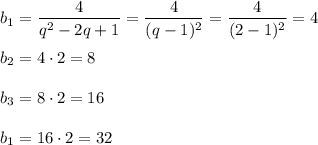
Объяснение:
16х-х²=0
это неполное квадратное уравнение
поэтому:
х(16-х)=0
х1=0
х2=-16
х²-4х+3=0
нужен дискриминант или Виета
(но Виета мы не проходили)
Д=(-4)²-4×1×3= 16-12=4
√д =2
х1 = (4+2)/2 =3
х2= (4-2)/2 = 1
5х² -6х + 1=0
аналогично
Д= 36 -4×5×1= 36-20=16
√д = 4
х1=(6+4)/5=2
х2=(6-4)/5=2/5
(х+4)² = 3х+40
тут нам нужно раскрыть формулу сначала
х²+8х+16=3х+40
переносим всё в одну сторону предварительно меняя знаки
х²+8х+16-3х-40=0
упрощаем
х²+5х-24=0
Д= 25+(4×1×24)= 25+96=121
√д = 11
х1= (-5+11)/2 = 3
х2=( -5-11)/2 =-8
х-7 3х-5
=
х. 2х
тут я бы использовал пропорцию т.е
2х(х-7)=х(3х-5)
2х²-14х=3х²-5х
перенос в одну сторону
-х²-9х=0
это неполное квадратное уравнение поэтому не вводим д
-х(х+9)=0
произведение равно 0 если хотябы один из множителей 0.
-х=0
х+9=0
х1=0
х2=-9
но 0 нельзя взять т.к у нас есть ОДЗ для дроби(на 0 делить нельзя)
ответ: х=-9
Надеюсь