Объяснение:
4(2x+7)=6x
8x+28=6x
x= -14
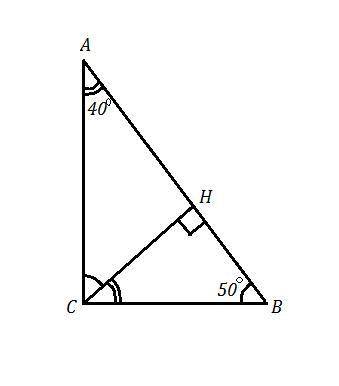
ΔАВС , ∠С=90° , ∠В=50° ⇒ ∠А=90°-∠В=90°-50°=40°
СН ⊥ АВ ⇒ ∠СНА=90° и ∠СРВ=90° .
Рассм. ΔВСН . Он прямоугольный и ∠В=50° , тогда ∠ВСН=90°-50°=40°. Это угол, образованный высотой СН с меньшим катетом (катет ВС лежит против меньшего острого угла ΔАВС).
Рассм. ΔАСН . Он прямоугольный и ∠А=40° , тогда ∠АСН=90°-40°=50°. Это угол, образованный высотой СН с бОльшим катетом АС (катет АС лежит против бОльшего острого угла ΔАВС).
Замечание. Так как у треугольников ΔАВС , ΔВСН и ΔАСН все три угла равны, то эти треугольники подобны .
Разделим знаменатели на 2
(2х+7)/3=х/2 - пропорция
(2х+7)*2=3х
4х+14=3х
х=-14 - это ответ.