1)
ОДЗ: 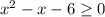 ⇒
⇒ 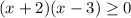 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
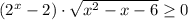 ⇔
⇔
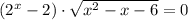 или
или 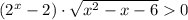
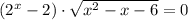 ⇒
⇒ 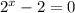 или
или 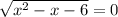 ⇒
⇒
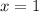 или
или  или
или 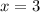
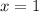 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 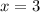
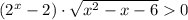 при
при ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
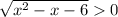 , тогда
, тогда 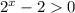 ⇒
⇒ 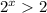 ⇒
⇒ 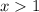
C учетом ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
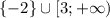
2)
ОДЗ: 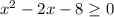 ⇒
⇒ 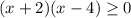 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
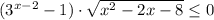 ⇔
⇔
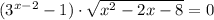 или
или 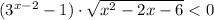
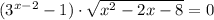 ⇒
⇒ 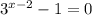 или
или 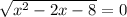 ⇒
⇒
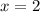 или
или  или
или 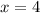
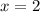 не входит в ОДЗ
не входит в ОДЗ
два корня  или
или 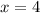
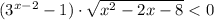 при
при ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
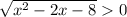 , тогда
, тогда 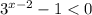 ⇒
⇒ 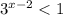 ⇒
⇒ 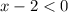
C учетом ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
![(-\infty;-2]\cup \{2\}](/tpl/images/1361/5355/83f26.png)
3)
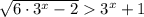
Так как 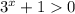 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
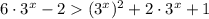
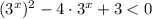
D=16-12=4
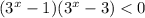
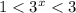
Показательная функция с основанием 3 возрастает
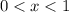
О т в е т. (0;1)
4)

Так как 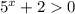 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
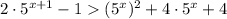
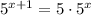
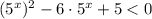
D=36-20=16
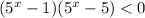
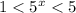
Показательная функция с основанием 5 возрастает
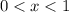
О т в е т. (0;1)
S= Vt
Тогда второй поезд:
S= 0.75V (t + 2.25)
т.к. 2 ч. 15 мин = 2 15/60 ч. = 2,25 ч.
100% - 25% = 75% = 75/100=0,75
Расстояние, которое поезда одинаковое.⇒
Vt = 0.75V(t+2.25)
Vt = 0.75Vt + 1.6875V
Vt - 0.75 Vt = 1.6875V
0.25Vt = 1.6875V
t= 1.6875V / 0.25V
t= 6.75 часа - время в пути первого поезда
6.75 +2.25 = 9 часов - время в пути второго второго поезда
7 ч. 00 мин. + 9 ч. = 16 ч. 00 мин. - второй поезд прибыл в Краснодар.
ответ: в 16 часов второй поезд прибыл в Краснодар.