Дана система уравнений:
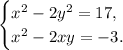
Из второго уравнения системы выразим 
через 
, получим:
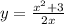--------(1)
Поскольку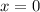 
не является корнем 2-го уравнения нашей системы, то подставив в первое уравнения системы вместо выражение (1), мы не потеряем решений системы:
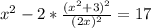, отсюда
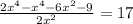, отсюда
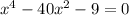---------(2)
Замена: пусть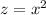 
, тогда (2) примет вид:
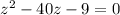--------(3)
(3) - квадратное уравнение относительно 
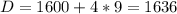
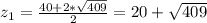
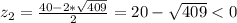
Но второй корень не удовлетворяет условию 
Возвращаясь к старой неизвестной, получим:
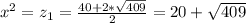-------(4)
Из (4) получаем два значения :
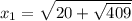
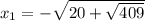
Подставим в первое уравнение системы вместо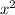 
выражение (4), найдем соответствующие значения :
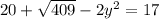, отсюда
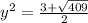--------(5)
Из (5) получаем два значения :
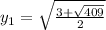
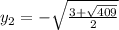
Итак, наша система имеет четыре решения:
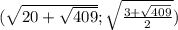
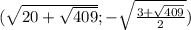
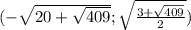
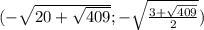
1. а)
(-4)(-2)(-0,5)(2)(5,5)(7)>X
D C M F K Z
б) F(2) и С(-2)
в) при перемещении на -6 точка F перейдет в точку с координатой 2-6 = -4 -точку D.
при перемещении на 5 точка F перейдет в точку с коорд. 2+5=7: - точку Z.
2. а) 3,6> -3,3 б) -6,2<-6 в) -56>-67 г) 0>-58.
3. а) | –3,8 | | –6,3 | = 3,8*6,3 = 23,94.
б) | –5,44 | : | 3,2 | = 5,44:3,2 = 1,7
4. а) х = -5,1 б) у = 17,6
5. 166 -(-23) -1 = 188 (-1 - потому что число 166 надо исключить из списка)
ответ: 188 целых решений
Объяснение:
а) (х + y)² = х² + 2хy + у² квадрат суммы
б) (5х – 3 )(5х + 3) = 25х² – 9 разность квадратов
в) (х – 2)( х² + 2х + 4) = х³ -8 разность кубов
г) (6х + у)² = 36 х² + 12хy + у² квадрат суммы
д) (х² – у )( х² + у) = х⁴ – y² разность квадратов
е) (х – 5)(х² + 5х + 25) = х³ – 125 разность кубов
3.Задание 2
Известно, что х² + 2хy + y² = 9, найдите:
а) (х + y)² = 9
б) (х + y)² – 5 = 4
в) (2х + 2y)² = 4х²+8ху+4у²=4(х² + 2хy + y²)=36
В примерах 1-5 раскройте скобки:
1. (х + 2у)²=х²+4ху+4у² квадрат суммы
2. (2а - З)²=4а²-12а+9 квадрат разности
3. (Зх - 5у²) (Зх + 5у²)=9х²-25у⁴ разность квадратов
4. (а + 2) (а² - 2а + 4)=а³+8 сумма кубов
5. (х + 1) (х² - х +1)=х³+1 сумма кубов