Решим задачу, выделяя 3 этапа математического моделирования:
1. Пусть х км/ч скорость велосипедиста, тогда (х+24) км/ч скорость мотоциклиста.
Расстояние между городами велосипедист проезжает за 7 часа, значит это расстояние выражается как 7х км.
Расстояние между городами мотоциклист проезжает за 4 часа, значит это расстояние выражается как 4(х+24) км.
Поскольку велосипедист и мjтоциклист проезжают одинаковое расстояние, то 4(х+24)=7х.
2. Преобразуем уравнение, раскрыв скобки:
4(x+24)=7x
4x+96=7x
7x-4x=96
3x=96
x=96:3
x=32
3. Получили, что х=32, значит, скорость велосипедиста 32 км/ч.
32+24=56 км/ч скорость мотоциклиста
7*32=224 км расстояние между городами
скорость велосипедиста 32 км/ч;
скорость мотоциклиста 56 км/ч;
расстояние между городами 224 км.
8; 18.
Объяснение:
Для решения данной задачи мы будем составлять систему из двух уравнений с двумя неизвестными.
Пусть Х и У - числа.
Сумма этих чисел - по условию - равна 26, то есть Х + У = 26.
Это первое уравнение системы.
Разность чисел - по условию - равна 10, то есть Х - У = 10.
Это второе уравнение системы.
Сведём вместе эти два уравнения в систему:
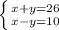
Решим данную систему сложения.
Имеем:
2*х = 36
х = 36 / 2
х = 18
Подставим найденное значение переменной Х в одно из уравнений, например, в первое уравнение составленной нами системы - для определения значения второй переменной:
х + у = 26
18 + у = 26
у = 26 - 18
у = 8
Мы нашли оба значения неизвестных - это числа 18 и 8.
Большее из них - 18. Меньшее - 8.
z'=cos(y-x^2)*2x
z''=-2x*sin(y-x^2)*2x+2cos(y-x^2)