Объяснение:
Докажите что выражение 4х -х²-5 приобретает только отрицательные значения.
-х² + 4х -5 = 0
D = 16 - 20 = -4 < 0
Уравнение не имеет решений. Следовательно, график функции у = 4х -х²-5 не пересекает ось абсцисс. Поскольку график представляет собой параболу, веточками вниз, то весь график расположен ниже оси абсцисс, то есть все значения выражения отрицательные. Наибольшее значение выражения находится в точке
х = -4 : (-2) = 2. При этом максимальное значение выражения ( в вершине параболы) равно -(2)² + 4 · 2 - 5 = -4 + 8 - 5 = -1
Утверждение доказано.
При умножении двух натуральных чисел их произведение было ошибочно увеличено на 372. При делении этого (ложного) произведения на меньший множитель получили в частном 90 с остатком 29. Найдите те числа.
1.
Пусть
- первый меньший множитель, причем ∈
.
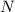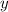- второй больший множитель число, причем ∈.
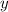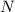Уравнение.
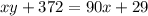
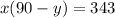
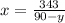
2.
Делители числа 343 это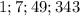 
, значит знаменатель 
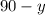может принимать эти значения:
1) 
=> 
=> 
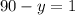Получаем первую пару возможных множителей: 
2) 
=> 
=> 
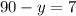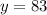Получаем вторую пару возможных множителей: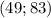 
3) 
=> 
=> 
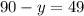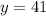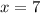
Получаем третью пару возможных множителей: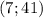 
4) 
=> 
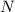∉ не является натуральным.
3.
Из трёх пар только в двух парах первый множитель будет меньшим.
1) Проверим пару :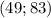
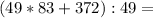
4439 : 49 = 90 (остаток 29) удовлетворяет условию.
2) Проверим пару :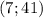
659 : 7 = 94 (остаток 1) не удовлетворяет условию.
ответ: 49; 83
1) 3х⁴–3х²у²=3х²*(х²-у²)=3х²*(х-у)(х+у)
2) 3х²–48ху + 192у²=3*(х²-16ху+64)=3*(х-8)²
3) х²+2ху+у²–64=(х+у)²-8²=(х+у-8)(х+у+8)
4) а³ + 27 – 3а – а²=(а+3)*(а²-3а+9) -а(а+3)=(а+3)*(а²-3а+9-а)=(а+3)*(а²+9-4а)
5) х³ – 3х² – 9х + 27=х²(х-3)-9*(х-3)=(х-3)*(х²-9)=(х-3)*(х-3)*(х+3)
(х-3)*(х-3)*(х+3)=0⇒х=±3