Действительных корней нет.
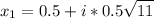
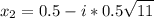
Объяснение:
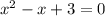
Это обычное квадратное уравнение. Решим его через дискриминант.
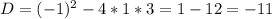
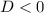следовательно действительных корней нет.
Найдем комплексные корни.
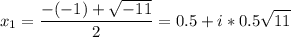
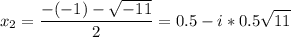
Теория:
Стандартный вид квадратного уравнения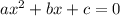 
, 
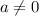
Дискриминант 
Если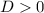 
, то квадратное уравнение имеет два действительных корня.
Если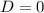 
, то квадратное уравнение имеет один действительных корень.
Если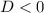 
, то квадратное уравнение не имеет действительных корней, однако комплексные корни существуют.
Комплексное число - число вида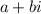 
, где 
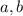- действительные числа,
- мнимая единица.
Мнимая единица - число, для которого выполняется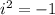 
Пусть х - число учеников, получивших "5" на экзамене. По условию, 90% процентов от этого количества посещают занятия. То есть посещавших и получивших "5" на экзамене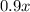
человек.
Пусть z - общее число учеников. По условию, 10% из них ходят на все занятия и получают "5". То есть этих людей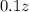
человек.
Таким образом, мы получили два выражения для тех, кто посещает занятия и получает "5":
Домножим обе части на 10:
Вероятность того, что случайно выбранный ученик получит "5" есть отношение числа учеников, получивших "5", к общему числу учеников:
ответ: 1/9