Составь математическую модель данной ситуации:
«Теплоход проходит расстояние между двумя пристанями по течению реки за 5 ч., а против течения - за 5,6 ч.
Собственная скорость теплохода — а км/ч, а скорость течения реки — m км/ч».
а) Определи скорость теплохода по течению реки и против течения реки.
Б) Определи расстояние, которое теплоход проплыл по течению реки.
с) Определи расстояние, которое теплоход проплыл против течения реки.
d) Сравни расстояние, пройденное теплоходом по течению реки и против течения реки.
Результат сравнения запиши в виде математической модели.
ления реки.
ответ:
а) скорость теплохода по течению реки — Окм/ч; против течения реки — Скм/ч;
b) расстояние, которое теплоход проплыл по течению реки:
с) расстояние, которое теплоход проплыл против течения реки:
d) расстояние, пройденное теплоходом по течению реки, и расстояние, пройденное теплоходом против течения
реки, будут (запиши прилагательное)
О-(O+O) C
O
-O-O) км.

👇

Открыть все ответы

Ответ:

Malika274

22.08.2022

A(a + 5b) - (a + b)(a - b)=a^2+5ab-a^2+b^2=5ab+b^2b(3a-b) - (a - b)(a + b)=3ab-b^2-a^2+b^2=3ab-a^2 (y+10)(y-2)-4y(2 - 3y)=y^2+8y-20-8y+12y^2=13y^2-20 (a-4)(a+9)-5a(1-2a)=a^2+5a-36-5a+10a^2=11a^2-36 (2b-3)(3b+2)-3b(2b+3)=6b^2-9b+4b-6-6b^2-9b=-14b-6 (3a-1)(2a-3)-2a(3a+5)=6a^2-2a-6a+4-6a^2-10a=-18a+4(m+3)^2 -(m-2)(m+2)=m^2+6m+9-m^2+4=5m+13(a-1)^ - (a+1)(a-2)=a^2-2a+1-a^2-a-2=-3a-1(c+2)(c--1)^2=c^2-c-6-c^2+2c-1=c-7 (y-4)(y+-3)^=y^2-16-y^2+6y-9=6y-25(a-2)(a++1)^ =a^2+2a-8-a^2-2a-1=-9(b-4)(b+-1)^=b^2-2b-8-b^2+2b-1=-9

4,5(81 оценок)

Ответ:

ТаяDuda2133

22.08.2022

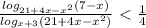
$\frac{log_{21+4x-x^2}(7-x)}{log_{x+3}(21+4x-x^2)} \ \textless \ \frac{1}{4}$
ОДЗ: 21 + 4x - x² > 0
21 + 4x - x² ≠ 1
7 - x > 0
x + 3 > 0
x + 3 ≠ 1

21 + 4x - x² > 0
x² - 4x - 21 < 0

x² - 4x - 21 = 0
По теореме Виета: x₁ = -3, x₂ = 7.

x² - 4x - 21 < 0
x ∈ (-3; 7)

21 + 4x - x² ≠ 1
x² - 4x - 20 ≠ 0
D = 16 + 80 = 96
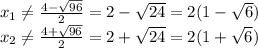
$x_1 \neq \frac{4- \sqrt{96}}{2} = 2 -\sqrt{24} = 2(1-\sqrt{6}) \\ x_2 \neq \frac{4+\sqrt{96}}{2} = 2+\sqrt{24}=2(1+\sqrt{6})$

7 - x > 0
x < 7

x + 3 > 0
x > -3

x + 3 ≠ 1
x ≠ -2

Окончательно, ОДЗ: x ∈ (-3; $2(1-\sqrt{6})$ ) U ( $2(1-\sqrt{6})$ ; -2) U (-2; $2(1+\sqrt{6})$ ) U ( $2(1+\sqrt{6})$ ; 7).

Решаем само неравенство:
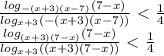
$\frac{log_{-(x+3)(x-7)}(7-x)}{log_{x+3}(-(x+3)(x-7))} \ \textless \ \frac{1}{4} \\ \frac{log_{(x+3)(7-x)}(7-x)}{log_{x+3}((x+3)(7-x))} \ \textless \ \frac{1}{4}$
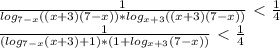
$\frac{1}{log_{7-x}((x+3)(7-x))*log_{x+3}((x+3)(7-x))} \ \textless \ \frac{1}{4} \\ \frac{1}{(log_{7-x}(x+3)+1)*(1+ log_{x+3}(7-x))} \ \textless \ \frac{1}{4}$
$\frac{1}{( \frac{1}{ log_{x+3}(7-x)}+1)*(1+ log_{x+3}(7-x))} \ \textless \ \frac{1}{4} \\ \frac{log_{x+3}(7-x)}{(1+ log_{x+3}(7-x))^2} \ \textless \ \frac{1}{4}$
Замена:
$t=log_{x+3}(7-x) \\ \frac{t}{(1+t)^2} \ \textless \ \frac{1}{4} \\ \frac{4t-(1+t)^2}{4(1+t)^2} \ \textless \ 0$
$\frac{4t-1-2t-t^2}{4(1+t)^2} \ \textless \ 0 \\ \frac{-(1-t)^2}{4(1+t)^2} \ \textless \ 0$
$\frac{(1-t)^2}{4(1+t)^2}\ \textgreater \ 0$
t ≠ 1
t ≠ -1
Делаем обратную замену:
$log_{x+3}(7-x) \neq 1 \\ log_{x+3}(7-x) \neq -1$

$7-x \neq x+3\\ 7-x \neq \frac{1}{x+3}$

$2x \neq 4\\ \frac{(7-x)(x+3)-1}{x+3} \neq 0$

$x \neq 2\\ \frac{20+4x-x^2}{x+3} \neq 0$

$x \neq 2\\ x^2-4x-20 \neq 0 \\ x+3 \neq 0$

$x \neq 2\\ x^2-4x-20 \neq 0 \\ x\neq -3$

Учитывая ОДЗ, окончательный ответ: x ∈ (-3; $2(1-\sqrt{6})$ ) U ( $2(1-\sqrt{6})$ ; -2) U (-2; 2) U (2; $2(1+\sqrt{6})$ ) U ( $2(1+\sqrt{6})$ ; 7).

4,4(6 оценок)

Это интересно:

Кулинария-и-гостеприимство

06.01.2020

Как сделать гуакамоле: рецепт и советы от профессионалов...

Финансы-и-бизнес

24.05.2021

Как получить бесплатные вещи без какого-либо мошенничества: советы и рекомендации...

Стиль-и-уход-за-собой

21.06.2021

Как блокировать удар: советы от профессионалов для самозащиты...

01.10.2020