1) если а=5, то корней нет
2) если а≠5, то х=3/(а-5)
3) бесконечного множества решений ни при каком а не существует
Объяснение:
ах-3=5х
ах-5х=3
х(а-5)=3
х=3/(а-5)
Если а-5=0, то есть а=5, то деление не имеет смысла, и корней нет.
Если а-5≠0, то есть а≠5, то, как уже найдено, х=3/(а-5).
Других случаев нет.
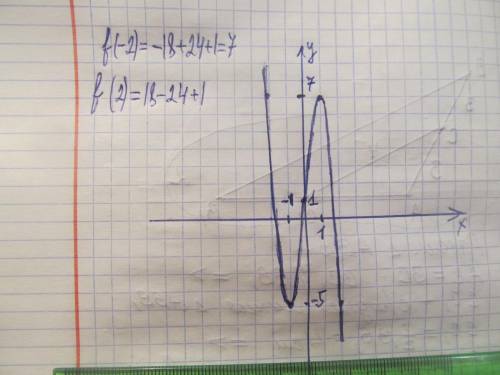
f(x)=-3x³+9x+1
f'(x)=-9x²+9=0 парабола ветвями вниз
x²-1=0; (x-1)(x+1)=0; критические точки х=1; х=-1
---------[-1]----------------------------[1]------------------>x
- + -
f(x) убывает min возрастает max убывает
f(-1)=-9+3+1=-5
f(0)=1
f(1)=9-3+1=7
f(-2)=7;
f(2)=-5
ф-ция убывает при х∈(-∞; -1) U (1; ∞)
ф-ция возрастает при х∈(-1; 1)
при х=-1 значение ф-ции минимально = -5
при х=1 максимально = 7
область определения (-∞; ∞)
область значений (-∞; ∞)
ф-ция общего вида.
1-й маляр покрасит фасад за 30 часов; 2-й маляр покрасит фасад за 20 часов
Объяснение:
Пусть объём работы будет равен 1 и пусть 1-й маляр покрасит фасад за х часов, а 2-й маляр - за у часов.
1/х - производительность 1-го маляра
1/у - производительность 2-го маляра
5 · 1/х + 4 · 1/у = 11/30
или
5/х + 4/у = 11/30 (1)
1/х + 1/у - общая производительность маляров
12 · (1/х + 1/у) = 1
или
1/х + 1/у = 1/12 (2)
Из уравнения (2) получим
1/у = 1/12 - 1/х (3)
Подставим (3) в уравнение (1)
5/х + 4(1/12 - 1/х) = 11/30
5/х + 1/3 - 4/х = 11/30
1/х = 11/30 - 1/3
1/х = (11 - 10)/30
1/х = 1/30
х = 30 (часов)
Из уравнения (3) найдём 1/у
1/у = 1/12 - 1/30
1/у = (5 - 2) /60
1/у = 3/60
1/у = 1/20
у = 20 (часов)
ax - 3 = 5x
ax - 5x = 3
(a - 5)x = 3
1) если a = 5 , то решений нет
2) если a ≠ 5 , то x = 3/(a - 5)
3) бесконечного множества решений не существует