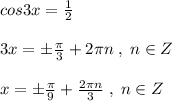
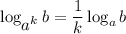 имеем , что
имеем , что 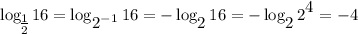
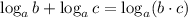 , получим что
, получим что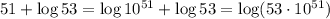
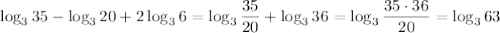
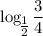 и
и 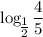
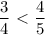 , то в силу монотонности функции(
, то в силу монотонности функции(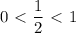 функция убывающая) имеем что
функция убывающая) имеем что 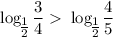
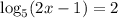
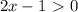 откуда
откуда 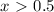
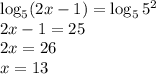
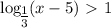
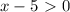 откуда
откуда 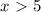
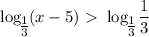
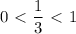 , функция убывающая, то знак неравенства меняется на противоположный
, функция убывающая, то знак неравенства меняется на противоположный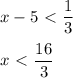
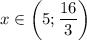
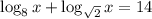
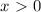
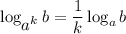 , получим что
, получим что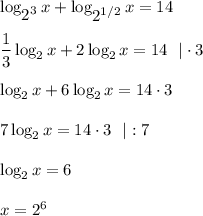
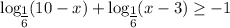
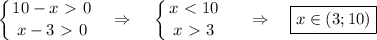
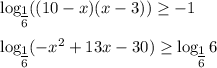
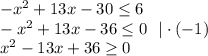
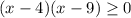 (*)
(*)![x \in (-\infty;4]\cup[9;+\infty)](/tpl/images/0366/9080/721ac.png)
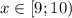 - ОТВЕТ.
- ОТВЕТ.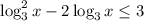
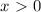
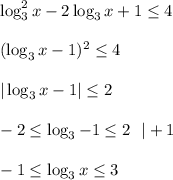
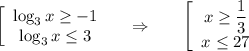
![x \in \bigg[\dfrac{1}{3} ;27\bigg].](/tpl/images/0366/9080/7e293.png)
Объяснение:
2. а14 равен 2,9,
а10 равен 0,5. Найдите первый член и разность этой арифметической прогрессии.
Решение. По формуле an=(n-1)в, находим:
а14=а1+13d;
а10=а1+9d;
2,9=а1+13d; [*(-1)]
0.5 =a1+9d;
-2.9=-a1-13d;
0.5=a1+9d;
Складываем:
-2,9+0,5=-13d+9d
-2.4=-4d;
d= 0.6;
Найдем a1:
0.5=a1+9*0.6;
0.5=a1+5.4;
a1=5.4-0.5=4.9.
a1=4.9.
***
3) Найдите сумму первых двадцати девяти членов арифметической прогрессии -3,5; -3,7;...
Решение.
а1=-3,5; а2= -3,7; ... d=-3.7 - (-3.5)= -3.7 + 3.5= - 0.2;
а29=-3.5 + (29-1) *(-0.2) = -3.5 +28*(-0.2)=-3.5 - 5.6 = - 9.1;
Сумма первых n членов арифметической прогресс равна
Sn= n*(a1+an) / 2.
S=29 * (a1+a29)/2 = 29*(-3.5 -9.1)/2 = 29* (-12.6)/2= - 365.4 / 2 = -182.7
S29= -182,7.
***
4) Сколько первых членов арифметической прогрессии
–12; -10; -8; ...
нужно сложить, чтобы получить -36?
Решение.
Sn=-36; a1=-12; d=-8 - (-10)=-8+10 = 2;
d=2;
an=a1+(n-1)d= -12+(n-1)*2= -12+2n-2= -14+2n;
Sn=n*(a1+an)/2;
-36=n*(-12-14+2n)/2;
-36=n*(-26+2n)/2;
-36=n*(-13+n);
-36=-13n+n²;
n²-13n +36=0;
По теореме Виета
n1+n2=13; n1*n2=36;
n1=9; n2=4;
a9=-12+8*2=-12+16=4;
a4=-12+3*2=-12 +6= -6;
S9=9*(-12+4)/2=9*(-8)/2=-72/2=-36;
S4=4*(-12+(-6))/2 = 4*(-18)/2 = -72/2=-36.
ответ: 9 или 4.
3. Найдите сумму первых двадцати девяти членов арифме-
тической прогрессии -3,5; -3,7;
4. Сколько первых членов арифметической прогрессии –12;
-10; -8; ... нужно сложить, чтобы получить -36?