1.Б
2.Г
3.В
4.А
Лишнее-Д.
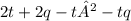
Ну, решать здесь нечего, так как это ни задача, ни неравенство, ни даже уравнение. Здесь можно только упростить, разложить на множители.
Видим, что у первый двух слагаемых есть общий множитель 2. А у вторых двух -t. Объединим одночлены в группы и вынесем общее. Если что, вынести общий множитель - значит разделить каждое слагаемое на него. Например, у 2t и 2q общий множитель 2. Чтобы вынести его за скобку, мы должны 2t поделить на 2 и 2q поделить на 2. То есть: 2t+2q=2(t-q). Можем себя проверить, умножив двойку на эту скобку. Получим тоже самое: 2*t+2*q. Таким образом:
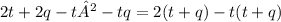
У t и q общее было - t. Мы разделили - t² и - tq на - t, получили t и q.
Теперь можем увидеть, что t+q - это общий множитель у получившихся слагаемых. Можем его тоже вынести, поделив 2(t+q) на t+q и - t(t+q) тоже делим на t+q. Получаем:
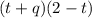
Это максимально упрощённое выражение.
Такое упрощение называют разложением многочлена на множители.
В решении.
Объяснение:
В двух коробках 28 упаковок бумаги. Если из первой коробки переложить во вторую 5 упаковок, то в первой коробке станет в 3 раза меньше упаковок бумаги, чем во второй. Сколько упаковок бумаги во второй коробке?
Решить задачу:
х - в первой коробке сначала.
у - во второй коробке сначала.
По условию задачи система уравнений:
х+у=28
3(х-5)=у+5
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=28-у
3х-15=у+5
3(28-у)-15=у+5
84-3у-15=у+5
-3у-у=5-69
-4у= -64
у= -64/-4
у=16 (упаковок) - во второй коробке сначала.
х=28-у
х=28-16
х=12 (упаковок) - в первой коробке сначала.
Теперь решить данные в условии уравнения и установить соответствия:
(Б) 3(х-5)=33-х
3х-15=33-х
3х+х=33+15
4х=48
х=48/4
х=12 (по решению задачи известно, что столько упаковок было в первой коробке изначально), условие самое нижнее, третье.
(А) 3(28-х)=х
84-3х=х
-3х-х= -84
-4х= -84
х= -84/-4
х=16 (по решению задачи известно, что столько упаковок было во второй коробке изначально), условие самое верхнее, первое.
(В) 3(23-х)=х+5
69-3х=х+5
-3х-х=5-69
-4х= -64
х= -64/-4
х=16 (по решению задачи известно, что столько упаковок было во второй коробке изначально), условие самое верхнее, первое.
Второму условия нет соответствия среди уравнений. По этому условию х должно быть равно 21 (16+5), такого ответа нет.
1. cosπ/6+cos5π/6=2cos(π/2)*cosπ/3=2*0*0.5=0 ответ Б
2.cosπ/6-cos5π/6=2sin(π/2)*sinπ/3=2*1*0.5√3 =√3 ответ Г
3. sinπ/6+sin3π/6=2sinπ/3*cosπ/6=2*0.5√3*0.5√3=3*0.5=1.5=3/2 ответ В
4. sinπ/6-sin3π/6=-2sinπ/6*cosπ/3=-2*0.5*0.5=-1/2 ответ А