ответ: Нет.
Из условия следует, что f(x) = (x – a)(x – b), где a ≠ b.
Пусть искомый многочлен f(x) существует.
Тогда, очевидно f(f(x)) = (x – t1)²(x – t2)(x – t3).
Заметим, что t1, t2, t3 — корни уравнений f(x) = a и f(x) = b, при этом корни этих уравнений не совпадают, поэтому можно считать, что уравнение f(x) = a имеет один корень x = t1.
Рассмотрим уравнение f(f(f(x))) = 0. Его решения, очевидно, являются решениями уравнений f(f(x)) = a и f(f(x)) = b. Но уравнение f(f(x)) = a равносильно уравнению f(x) = t1 и имеет не более двух корней, а уравнение f(f(x)) = b — не более четырех корней (как уравнение четвертой степени).
То есть уравнение f(f(f(x))) = 0 имеет не более 6 корней.
1) у=(1/3)х+2 1/3
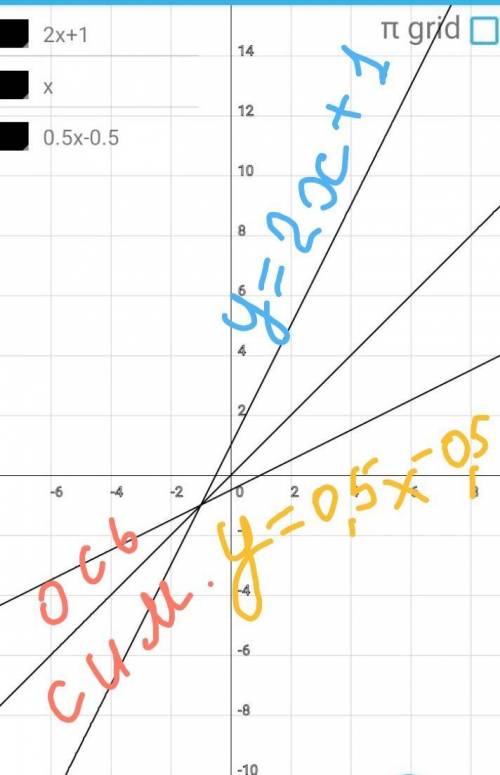
2) у=0,5х-0,5
Объяснение:
1.
у=3х-7
-3х=-у-7
Выразим х через у:
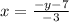
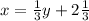
Поменяем местами х и у:
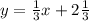
Это уравнение обратной функции.
2.
у=2х+1
Выразим х через у:
-2х=-у+1
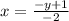
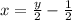
Поменяем местами х и у:
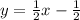
у=0,5х-0,5
Это уравнение обратной функуии.
3.
Известно, что графики прямой и
обратной функций симметричны
относительно биссектрисы 1 коор
динатной четверти.
В одной систеие координат пост
роим графики прямой и обратной
функций. Оба графика - прямые
линии, поэтому достаточно запол
нить таблицу для двух точек.
Таблица для прямой функции:
х 0 2
у -7 -1
Таблица для обратной функции"
х -6 3
у 1/3 1
Оба графика строим в одной ко
ординатной плоскости.
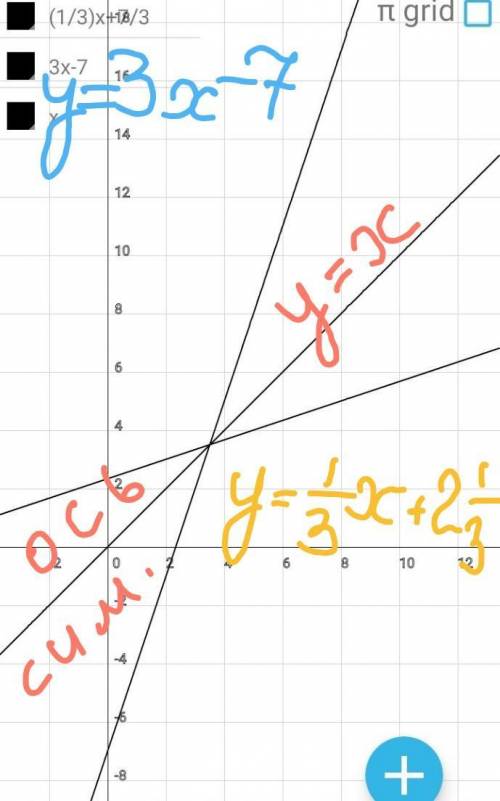
a-b
Объяснение:
b^2-a^2: модуль а может быть меньше чем модуль b
(b-a)^3: отрицательное - положительное = отрицательное. степень не парный. он в любом случае будет отрицательным
a^4-b^4: модуль а может быть меньше чем модуль b
a-b: минус на минус даёт плюс, поэтому это выражение всегда принимает положительные значения