ответ: 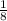
Объяснение:
Количество элементарных исходов равно 64, так как по формуле размещений с повторениями 8*8=64. Количество элементарных исходов, благоприятствующих событию, описываемому в задаче равно 8, это число можно получить перебором.
Число делится на 9, если сумма его цифр делится на 9. Сумма цифр двузначного числа, делящегося на 9, может равняться либо 9, либо 18. По условию задачи, цифры меньше 9, значит, сумма цифр не может быть равна 18 (9+9=18). Значит, нужно рассмотреть все двузначные числа, в которых сумма цифр равна 9. Это числа: 18, 27, 36, 45, 54, 63, 72, 81.
Так как нет оснований полагать, что каким-либо цифрам было отдано предпочтение, то есть, вероятность любого числа, написанного на доске, одинакова, то здесь применима формула, называемая классическим определением вероятности, согласно которой вероятность нужного нам события равна отношению количества благоприятствующих событию исходов к общему количеству исходов, то есть, 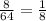 .
.
Лексель Котов – архимагос исследовательского флота Котова
Таркис Блейлок – фабрикатус-локум, магос региона Кебрения
Виталий Тихон – звёздный картограф орбитальных галерей Кватрии
Линья Тихон – звёздный картограф, дочь Виталия Тихона
Азурамаджелли – магос астронавигации
Криптаэстрекс – магос логистики
Тарентек – фабрикатус ковчега
Хиримау Дахан – секутор/сюзерен гильдии
Хирона Манубия – магос кузни “Электрус”
Тота Мю-32 – надсмотрщик Механикус
Авреем Локк – крепостной
Расселас Х-42 – аркофлагеллант
Ванн Койн – крепостной
Юлий Хоук – крепостной
Исмаил де Рёвен – сервитор
Галатея – запрещённый машинный интеллект
Экснихлио
Веттий Телок – архимагос исследовательского флота Телока
“Ренард”
Робаут Сюркуф – капитан
Эмиль Надер – первый
Адара Сиаваш – наёмный стрелок
Иланна Павелька – техножрец
Каирн Силквуд – технопровидец
1/8 ( 0,125 )
Объяснение:
Чтобы число делилось на 9 сумма его цифр должна делиться на 9.
Всего двузначных чисел мы можем составить 64 ( = 8 * 8 ).
Возможные суммы цифр среди них: 1,2,3,...16.
Из них лишь одна сумма делится на 9 - 9. Комбинаций для получения данной суммы цифр всего 8 (1;8) (8;1) (2;7) (7;2) (3;6) (6;3) (4;5) (5;4).
P = m/n; n = 64; m = 8; p = 1/8