аргумент комплексного числа argz - это угол между вектором, соответствующим этому комплексному числу, если изобразить его на комплексной плоскости, и положительным направлением оси ох; если считать угол против часовой стрелки, от оси к вектору, то угол будет со знаком +, если считать по часовой стрелке, то угол нужно брать со знаком -.
z = 1 - i это вектор, координаты его имеют вид (1 ; -1).
верны соотношения для угла fi = arg z:
cos fi = x / |z|
sin fi = y / |z|
здесь |z| = sqrt(x^2 + y^2) - модуль комплексного числа z (он же - длина вектора с координатами (x; y), где z = x + yi )
таким образом, получаем, |z| = sqrt ( 1^2 + (-1)^2 ) = sqrt 2
cos fi = 1 / sqrt 2
sin fi = -1 / sqrt 2
такой угол - это -pi/4
arg z = -pi/4
1)
ОДЗ: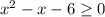
⇒ 
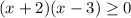⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
два корня
или 
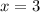
C учетом![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
получаем ответ:
2)
ОДЗ: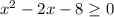
⇒ 
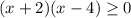⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
два корня
или 
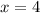
C учетом![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
получаем ответ:
3)
Так как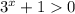
при любых х, возводим данное неравенство в квадрат:
D=16-12=4
Показательная функция с основанием 3 возрастает
О т в е т. (0;1)
4)
Так как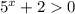
при любых х, возводим данное неравенство в квадрат:
D=36-20=16
Показательная функция с основанием 5 возрастает
О т в е т. (0;1)