Question

Знайдіть усі пари чисел p і q, що 3p^4 +5q^4+15=13p^2*(q^2)

Answer 1

$3p^4 +5q^4+15=13p^2*q^2\\ 0+2q^4+0\equiv p^2q^2(mod\;3)\\ q^2(2q^2-p^2)\equiv 0(mod\;3)\\$

Т.к. 3 простое, то либо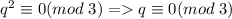 $q^2\equiv 0(mod\;3)=q\equiv0(mod\;3)$ (1), либо 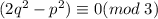$(2q^2-p^2)\equiv 0(mod\;3)$ (2).

Число может давать один из трех остатков 0, 1, 2 при делении на 3. Тогда

$a\equiv0(mod\;3)=a^2\equiv0(mod\;3)\\ a\equiv1(mod\;3)=a^2\equiv1(mod\;3)\\ a\equiv2(mod\;3)=a^2\equiv2*2(mod\;3)\equiv1(mod\;3)$

Т.е. квадрат натурального числа дает один из двух остатков 0, 1 при делении на 3.

Тогда для (2) единственный вариант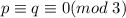 $p\equiv q \equiv 0 (mod \;3)$ . В случае (1) же получили, что 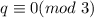$q\equiv0(mod\;3)$ . А значит в любом случае $q\equiv0(mod\;3)$ .

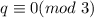Т.к. оно простое, то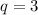 $q=3$

$p^4 +5*27+5=13p^2*3\\ (p^2)^2-39*p^2+140=0\\ p^2=\dfrac{39\pm\sqrt{39^2-4*140}}{2}=\dfrac{39\pm\sqrt{1600+1-80-560}}{2}=\dfrac{39\pm\sqrt{961}}{2}=\dfrac{39\pm31}{2}\\ p^2=4\;\;\;\;\;\;\;\;\;\;\;\;p^2=35\\ p=\pm2\;\;\;\;\;\;\;\;\;\;\;\;p=\pm\sqrt{35}$

p простое =>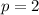 $p=2$

ответ: (2;3)

___________________________________________

Использованы свойства сравнения чисел по модулю