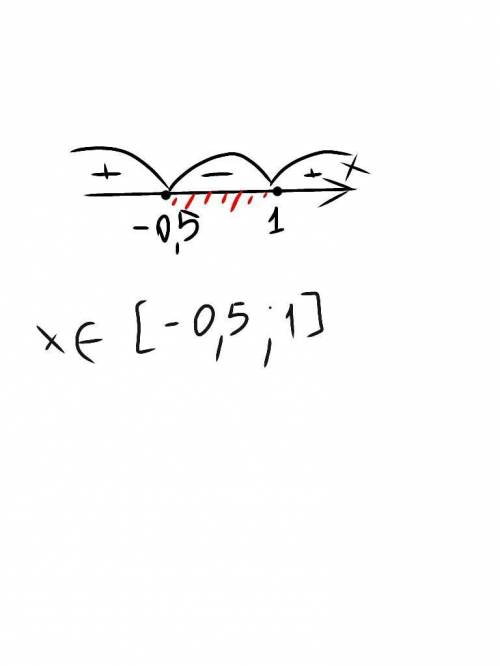
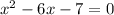
Значение квадратного уравнения.
Решение:для 8 класса (через дискриминант):
Вспоминаем вид уравнения, при котором можно вычислить дискриминант: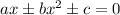 
.
То есть наше уравнение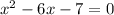 
, где 
, 
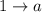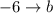и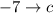 
.
Вспоминаем формулу нахождения дискриминанта: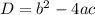 
.
⇒ 
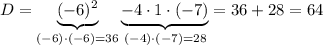
Вы (очень надеюсь) знаете, что есть правила дискриминанта:
Поскольку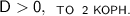 
Вспоминаем формулу нахождения корней уравнения:
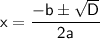⇒ Найдём корни нашего уравнения:
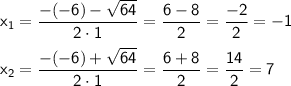
для 7 класса (через разложение трёхчлена):
Представим член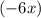 
в виде выражения 
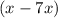и запишем его в уравнение:
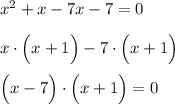
Произведение равно 0, если один из множителей равен 0.
.
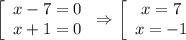
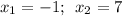ответ: 168=4*(7+а8) или 7+а8=42 или а8=35. Тогда разность равна (35-7)/7=4.
ответ 4.
Объяснение: