Объяснение:
1. E
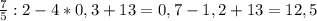
2. Д
4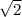 +21
+21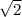 -8
-8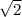
3. Д
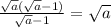
4. В
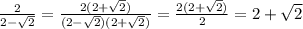
5. А
x(2x-7)=0 x=0 или x=3,5
6. В
D=9-4*2*(-5)=49
7. В
D=1-4*1*(-20)=81
x1=(-1+9)/2=4 x2=(-1-9)/2=5
8. А
4y²-12y+9=y²+4y+4
3y²-16y+5=0
D=14² y1=5 y2=1/3
9. С
D=81-4*5*(-2)=121
x1=(9+11)/10 x1=2 x2=(9-11)/10=-0,2
сумма корней: 2-0,2=1,8
10. нет корней , в записи уравнения ошибка видимо в знаке
11. Д
Приводим к общему знаменателю, при этом знаменатель не равен 0 и отбрасываем его, приравниваем числитель к 0:
5y²-15y-4y²+8y-y(y²-5y+6)=0
-y³+6y²-13y=0
y(y²-6y+13)=0 y≠0 по ОДЗ и второе уравнение не имеет корней
12. А
Пользуемся формулой ax²+bx+c=a(x-x1)(x-x2)
легко найти корни: x1=-5 и x2=1/3 подставляем:
3(x-(-5))(x-1/3)= заносим 3 во вторую скобку: (x+5)(3x-1)
Объяснение:
1. E
2. Д
4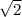 +21
+21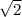 -8
-8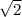
3. Д
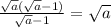
4. В
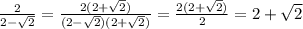
5. А
x(2x-7)=0 x=0 или x=3,5
6. В
D=9-4*2*(-5)=49
7. В
D=1-4*1*(-20)=81
x1=(-1+9)/2=4 x2=(-1-9)/2=5
8. А
4y²-12y+9=y²+4y+4
3y²-16y+5=0
D=14² y1=5 y2=1/3
9. С
D=81-4*5*(-2)=121
x1=(9+11)/10 x1=2 x2=(9-11)/10=-0,2
сумма корней: 2-0,2=1,8
10. нет корней , в записи уравнения ошибка видимо в знаке
11. Д
Приводим к общему знаменателю, при этом знаменатель не равен 0 и отбрасываем его, приравниваем числитель к 0:
5y²-15y-4y²+8y-y(y²-5y+6)=0
-y³+6y²-13y=0
y(y²-6y+13)=0 y≠0 по ОДЗ и второе уравнение не имеет корней
12. А
Пользуемся формулой ax²+bx+c=a(x-x1)(x-x2)
легко найти корни: x1=-5 и x2=1/3 подставляем:
3(x-(-5))(x-1/3)= заносим 3 во вторую скобку: (x+5)(3x-1)
(см. объяснение)
Объяснение:
Шаг 1: преобразуем уравнение.
Шаг 2: выполним замену.
Замена:
ОДЗ для буквы t:
Sin дает значения от -1 до 1 включительно. Если умножить их на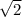 , то получится, что
, то получится, что ![t\in\left[-\sqrt{2};\; \sqrt{2}\right]](/tpl/images/1104/3279/ec516.png) ,
,
Шаг 3: решим квадратное уравнение.
Продолжим решение:
Рассмотрим корень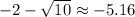 (а вообще понятно, что само число больше, чем корень из него, а тут мы еще корень из 10 вычитаем). Он посторонний, так как выше мы доказали, что
(а вообще понятно, что само число больше, чем корень из него, а тут мы еще корень из 10 вычитаем). Он посторонний, так как выше мы доказали, что ![t\in\left[-\sqrt{2};\; \sqrt{2}\right]](/tpl/images/1104/3279/ec516.png) . Другой корень посторонним не является. Значит работать будем только с ним.
. Другой корень посторонним не является. Значит работать будем только с ним.
Шаг 4: обратная замена.
Обратная замена:
Выше уже узнавали значение суммы sin и cos через одну тригонометрическую функцию. Поэтому пишу сразу:
Полученное уравнение можно без труда решить следующим образом:
Уравнение решено!