Объяснение:
a1=68; a2=58
d=a2-a1=58-68=-10
a3=a2+d=58-10=48
ответ: 48
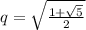
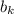 - k-ый ((n-k)+1)-ый
- k-ый ((n-k)+1)-ый 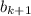 - (k+1)-ый (n-k)ый
- (k+1)-ый (n-k)ый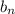 - n-ый обратный счет вверх 1-ый
- n-ый обратный счет вверх 1-ый
48
Объяснение:
a2-a1=68-58=10