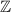 разделим на три класса:
разделим на три класса: , где + обозначает операцию объединения и изначает, что множества
, где + обозначает операцию объединения и изначает, что множества 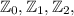 дисъюнктны.
дисъюнктны.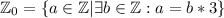
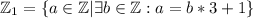

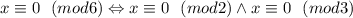
 .
.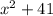 делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3:
делится на два (сумма нечетных чисел четна), то есть выражение все равно делится на два, первое условие выполнено. Докажем, что x делится на 3: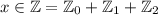 , то рассмотрим три случая:
, то рассмотрим три случая: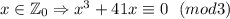 так как
так как 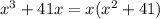 .
.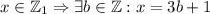
 для каких-то
для каких-то  , то есть
, то есть 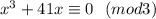 .
.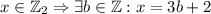 .
.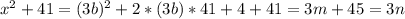 для каких-то
для каких-то  , то есть
, то есть 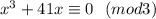 .
.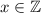 выражение
выражение 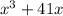 делится на 6.
делится на 6.
1. Сложение векторов AB + BC определяется из правила параллелограмма.
Путем параллельного переноса соединить начала обоих векторов в одной точке, достроить до параллелограмма. Диагональ параллелограмма является суммой двух векторов
Диагонали в точке пересечения M делятся пополам, т.е.
2) Длину вектора ВС можно найти по теореме Пифагора из прямоугольного треугольника ABM, в нем |BM|=|BD|/2 = 8 см; |AM| = 6 см
3) Для начала найдем координаты вектора АС:
2. 1) Координаты вектора АС: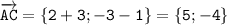
Длина вектора АС: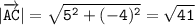 см
см
2) Координаты вектора BD: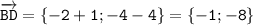
Длина вектора BD: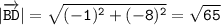 см
см
3.CT || AM || BP как перпендикулярны к одной прямой, значит четырехугольник AMTC - прямоугольная трапеция, BP - средняя линия трапеции, следовательно