В решении.
Объяснение:
Выберите систему уравнений, соответствующую условию задачи: расстояние от поселка до города 62 км;
велосипедист и мотоциклист, выехав одновременно навстречу друг другу, встречаются через час.
Найдите скорость велосипедиста и мотоциклиста, если скорость велосипедиста на 28 км/ч меньше, чем скорость мотоциклиста.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость велосипедиста.
у - скорость мотоциклиста.
1) х + у = 62
у - х = 28
х = 62 - у
у - 62 + у = 28
2у = 90
у = 45 (км/час) - скорость мотоциклиста.
45 - 28 = 17 (км/час) - скорость велосипедиста.
Второй вариант:
х - скорость мотоциклиста.
у - скорость велосипедиста.
4) х + у = 62
х - у = 28
х = 62 - у
62 - у - у = 28
-2у = 28 - 62
-2у = -34
у = -34/-2
у = 17 (км/час) - скорость велосипедиста.
х = 62 - 17
х = 45 (км/час) - скорость мотоциклиста.
Можно использовать две системы на выбор, в зависимости от обозначений. ответ не изменится.
1) х+у=62
у-х=28
2) х+у=28
х-у=62
3) х+у=28
у-х=62
4) х+у=62
х-у=28
Сначала разберёмся что такое медиана чисел.
Медианой чисел называется число, стоящее посередине упорядоченного по возрастанию ряда чисел — в случае, если количество чисел нечётное. Если же количество чисел в ряду чётно, то медианой ряда является полусумма двух стоящих посередине чисел упорядоченного по возрастанию ряда.
Упорядочим ряд. Получим:
2,4; 2,4; 2,6; 2,7; 2,7; 3,0
Количество чисел в ряду чётное, значит медиана будет равна полусумме центральных чисел:
2,4; 2,4; 2,6; 2,7; 2,7; 3,0
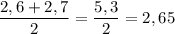
ответ: медиана данного ряда равна 2,65.
48
Объяснение:
Представить в виде степени (36 в виде степени с основанием 6, 4 в виде степени с основанием 2)
(6^(2n))/(3^(2n-1)*2^(2n-4))
Разложить выражение на множители (6 разложить на 3*2)
(3^(2n)*2^(2n))/(3^(2n-1)*2^(2n-4))
Упростить выражение (3^2n сокращаем с 3^(2n-1), в числителе остаётся 3, в знаменателе 1) (2^2n сокращаем с 2^(2n-4), в числителе остаётся 2^4, в знаменателе 1)
3*2^4
Вычислить степень
3*16
Умножьте числа
48