5)
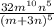- при возведении степени в степень, их показатели перемножаются, к примеру (2^2)^2 = 2^4 = 16, когда мы взяли в 5 степень, нужно и числитель и знаменатель возвести в 5 степень, числитель по принципу который я описал выше, а знаменатель это сумма, поэтому мы просто возводим сумму в 5 степень, но не раскрываем, так как от нас это не требуется и это выходит за рамки 9 класса)
7)
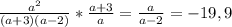
Знаменатель нужно разложить по формуле, a(x-x1)(x-x2), где a это коэффициент перед x^2, а x1,x2 это корни уравнения, чтобы их найти решаем, как нам удобно, тут легко подойдет т.виетта - корни -3;2, после разложения видим, что сокращается скобка a+3, а в числителе у нас сокращается квадрат у a (сокращаем крест на крест), получаем выражение a/a-2, подставляем и считаем, все)
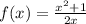
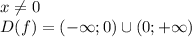
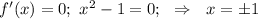
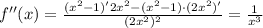
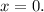
вт. Отвееет