В равностороннем треугольнике все стороны равны и каждый угол равен 60°. Также в равностороннем треугольнике все высоты равны, так что найдём любую. Проводим высоты. В равностороннем треугольнике высота является медианой и биссектрисой. Таким образом высота делить сторону длиной
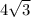
На два равны отрезка. Получим прямоугольный треугольник (так как у гол между сторону и высотой, проведённой к данной стороне равен 90°), у которого катет и гипотенуза равны
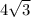
И
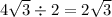
Соответственно, пусть высота равна h, тогда по теореме Пифагора
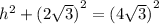
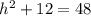
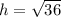
h = 6
ответ: 6
|x−3|≤7; -7≤x−3≤7; [-4;10], длина отрезка 14
|x−5|≥7; x−5≥7 или x−5≤-7; (−∞;-2]∪[12;+∞).
Длина пересечения решений - длина отрезка [-4;-2] равна 2.
Искомая вероятность равна отношению 2/14≈0.29