Сначала решаем соотв. однородное уравнение, запишем его характеристическое уравнение
\lambda^2-6\lambda+9=0λ
2
−6λ+9=0
имеем случай кратных действительных корней, значит общее решение однородного уравнения
y(x)=C_1*e^{3x}+C_2*x*e^{3x}y(x)=C
1
∗e
3x
+C
2
∗x∗e
3x
Далее применим метод вариации. Тогда
\begin{gathered} \left( < br / > \begin{array}{cc} < br / > e^{3 x} & e^{3 x} x \\ < br / > 3 e^{3 x} & 3 x e^{3 x}+e^{3 x} \\ < br / > \end{array} < br / > \right) * \left( < br / > \begin{array}{c} < br / > C_1'(x) \\ < br / > C_2'(x) \\ < br / > \end{array} < br / > \right)=\left( < br / > \begin{array}{c} < br / > 0 \\ < br / > 9 x^2-12 x+2 \\ < br / > \end{array} < br / > \right) \end{gathered}
⎝
⎛
<br/>
<br/>e
3x
<br/>3e
3x
<br/>
e
3x
x
3xe
3x
+e
3x
<br/>
⎠
⎞
∗
⎝
⎛
<br/>
<br/>C
1
′
(x)
<br/>C
2
′
(x)
<br/>
<br/>
⎠
⎞
=
⎝
⎛
<br/>
<br/>0
<br/>9x
2
−12x+2
<br/>
<br/>
⎠
⎞
Откуда получим
C_1'(x)=-e^{-3x}*x*(9x^2-12x+2), < br / > C_2'(x)=e^{-3x}*(9x^2-12x+2)C
1
′
(x)=−e
−3x
∗x∗(9x
2
−12x+2),<br/>C
2
′
(x)=e
−3x
∗(9x
2
−12x+2)
Интегрированием находим
C_1(x)=-e^{-3 x}(x^2 - 3 x^3)+A, C_2(x)=e^{-3 x} (2 x - 3 x^2)+BC
1
(x)=−e
−3x
(x
2
−3x
3
)+A,C
2
(x)=e
−3x
(2x−3x
2
)+B
Следовательно общее решение уравнения запишется как (переобозначим константы A и B )
y(x)=(-e^{-3 x}(x^2 - 3 x^3)+C_1)*e^{3x}+(e^{-3 x} (2 x - 3 x^2)+C_2)*x*e^{3x}y(x)=(−e
−3x
(x
2
−3x
3
)+C
1
)∗e
3x
+(e
−3x
(2x−3x
2
)+C
2
)∗x∗e
3x
или
y(x)=C_1*e^{3x}+x*C_2*e^{3x}+x^2y(x)=C
1
∗e
3x
+x∗C
2
∗e
3x
+x
2
Соотв. постоянные для нашей задачи Коши находятся из системы
\left \{ {{y(0)=0} \atop {y'(0)=3}} \right.{
y
′
(0)=3
y(0)=0
Откуда
\left \{ {{C_1=0} \atop {C_2=3}} \right.{
C
2
=3
C
1
=0
16%
Объяснение:
допустим исходная стоимость товара х
x* 3/5 идет с наценкой 5%. то есть этот товар стал стоить на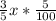
дороже. то есть цена этого товара стала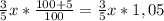 
Осталость 2/5 товара. Половина его, то есть 1/5 продавалась с наценкой 4%, то есть она стоила 1,04x*1/5
Оставшиеся 1/5 товара продавалист с неизвестной наценкой y%, она стоила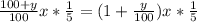
В итоге товар стоил
1,05*x*3/5 + 1,04*x*1/5 + (1+y/100))*x*1/5= (1,05*3+1,04 +(1+y/100)x/5
с другой сторны общая наценка оказалась 7%, то есть товар стал стоить 1,07х
Получаем уравнение
(1,05*3+1,04 +(1+y/100))x/5=1,07х
Сокращаеи на х
(1,05*3+1,04 +(1+y/100))/5=1,07
1,05*3+1,04 +(1+y/100)=1,07*5
3,15+1,04 +1 +y/100=5,35
5,19 +y/100=5,35
y/100=0,16
y=16