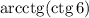
Известно соотношение:
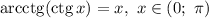
Кроме этого, известно, что основной период котангенса равен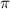 
:
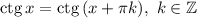
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида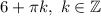 
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
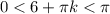
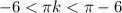
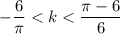
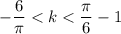
Выполним оценку обеих частей неравенства:
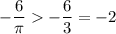
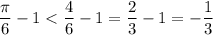
Получим:
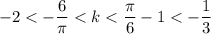
Или записывая соотношение для k:
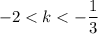
Единственное подходящее целое значение: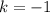 
.
Запишем:
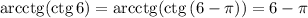
Действительно, 
, арккотангенс может принимать такое значение.
ответ: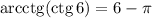 
y₁ = x² - 4x + 3; y₂ = x - 1
исследуем функцию y₁ = x² - 4x + 3
Нули функции:
x² - 4x + 3 = 0
D = 16 - 12 = 4
√D = 2
x₁ = (4 - 2):2 = 1
x₂ = (4 + 2):2 = 3
Вершина параболы: х = 4/2 = 2
у(2) = 4 - 4·2 + 3 = -1
Для определения пределов интегрирования найдёи точки пересечения функций
y₁ = x² - 4x + 3 и y₂ = x - 1
x² - 4x + 3 = х - 1
x² - 5x + 4 = 0
D = 25 - 16 = 9
√D = 3
x₁ = (5 - 3):2 = 1
x₂ = (5 + 3):2 = 4
Итак, нижний предел интегрирования x₁ = 1, верхний - x₂ = 4
Поскольку на интервале х∈(1,4) у₂ > у₁, то будем находить интеграл от разности
у₂ - у₁ = x - 1 - (x² - 4x + 3) = x - 1- x² + 4x - 3 = - x² + 5x - 4
∫(- x² + 5x - 4)dx = -x³/3 + 5x²/2 - 4x
Подставим пределы интегрирования
S = (-64/3 + 5·16/2 - 4·4) - (-1/3 + 5/2 - 4) = -64/3 + 40 - 16 +1/3 - 5/2 + 4 =
= - 21 + 28 - 2,5 = 4,5
2) (1;-4)
3) у=-2х+3
4) Думаю, что не нужно объяснять, что это прямая.