1) Аналитический.
2) Рекуррентній.
3) Это арифметическая прогрессия с разностью –5. Продолжается так: 6,7; 6,2; 5,7; 5,2; 4,7; 4,2; 3,7; 3,2 ...
4) Первое число кратное трём, это тройка. Поэтому подходят либо второй, либо третий вариант. Четвёртый член должен быть равен 3*4=12, поэтоу правильный ответ — второй: 3; 12; 33.
5)
6)
7) Это арифметическая прогрессия.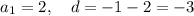 
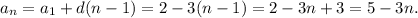
8)
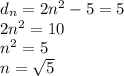
ответ: нет, не является, потому что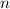 
должно быть натуральным числом.
9) 
Наибольшее натуральное 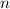, удовлетворяющее этому неравенству, — это 16.
ответ: 16 членов.
10)
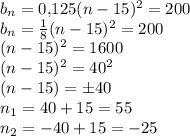
Второе решение не подходит, поскольку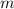 
должно быть натуральным числом.
ответ: 
а) (2m)^2 + 2m + 1 = 4m^2 + 2m + 1 = 2(2m^2+m) + 1, где 2m^2+m натуральное (в силу того, что произведение и сумма натуральных числе всегда натуральна), будет нечётным.
(2m+1)^2 + (2m+1) + 1 = 4m^2 + 4m + 1 + 2m + 1 + 1 = 4m^2 + 6m + 2 + 1 =
2(2m^2 + 3m + 1) + 1, где 2m^2 + 3m + 1 натуральное, будет нечётным.
b) Квадрат чётного числа - чётный. Потому число n^2 + n + 1 не может быть квадратом чётного числа.
Покажем, что число не может быть и квадратом нечётного числа:
n^2 + n + 1 = n^2 + 2n + 1 - n = (n+1)^2 - n
Т.е. число n^2 + n + 1 отличается от квадрата (n + 1)^2 на n единиц. Может ли такое число быть квадратом?
(n + 1)^2 - n^2 = n^2 + 2n + 1 - n^2 = 2n + 1 > n
Не может.
Цельная и стройная запись решения:
n^2 < n^2 + n + 1 = (n + 1)^2 - n < (n + 1)^2
Т.к. число n^2 + n + 1 лежит между двумя квадратами последовательных натуральных чисел, само оно не может быть квадратом натурального числа.