1)1. Выразить у через х(или наоборот) из одного уравнения системы.
2. Подставить полученное выражение вместо у(х) в другое уравнение системы.
3. Решить полученное уравнение относительно х(у).
4. Подставить поочередно каждый из найденных на третьем шаге корней уравнения вместо х(у) в выражение у(х) через х(у), полученное на первом шаге.
5. Записать ответ в виде пар значений (х; у), которые были найдены соответственно на третьем и четвертом шаге.
2)Привести два уравнения системы к одинаковым по модулю коэффициентам при переменной х или при переменной у.
Если коэффициенты одинаковые, то из одного уравнения вычесть другое. Если же коэффициенты противоположные по значению, то уравнения системы складываются.
Решить полученное уравнение относительно одной переменной и найти значение одной из переменных системы
.
Выразить из одного из уравнений системы неизвестную переменную.
Подставить известное значение и найти значение второй переменной.
Записать ответ.
а) f'(x)=3x^2-27
3x^2-27=0
x^2=9
x=±3
f'(x)>0 при х∈(-∞;-3)∨(3;+∞)
b) f'(x)=8x^3-1
8x^3-1=0
x^3=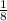
x=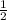
f'(x)>0 при х∈(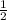 ;+∞)
;+∞)
c) f'(x)=3x^2-4
3x^2-4=0
x^2=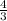
x=±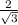
f'x>0 при х∈(-∞;-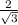 )∨(
)∨(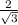 ;+∞)
;+∞)