Question

Найдите сумму решений уравнения tg2x * cos2x = sin2x + sin4x, принадлежащих множеству [-п; 2п]

Answer 1

Перепишем уравнение, учитывая, что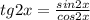 $tg2x=\frac{sin2x}{cos2x}$

$\frac{sin2x}{cos2x}*cos2x=sin2x+sin4x$ -----(1)

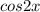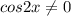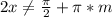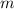В уравнение (1) выражение $cos2x$ находится в знаменателе, поэтому $cos2x\neq0$, или  $2x\neq\frac{\pi}{2}+\pi*m$, $m$ - целое

или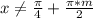  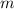$x\neq\frac{\pi}{4}+\frac{\pi*m}{2}$, $m$ - целое-----(2)

Сократим в левой части уравнения (1) на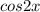 $cos2x$:

  $sin2x=sin2x+sin4x$, отсюда $sin4x=0$, отсюда

  $4x=\pi*n$, или $x=\frac{\pi*n}{4}$, $n$ - целое ------(3)

Из решений (3) надо исключить значения, равные значениям (2):

 $x=\frac{\pi*n}{4}\neq\frac{\pi}{4}+\frac{\pi*m}{2}$, отсюда

  $\pi*n\neq\pi+2\pi*m$, сокращая на $\pi$, получим

  $n\neq1+2*m$ - нечетные числа 

Другими словами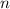 $n$ принимает только четные значения!

 Из условия следует, что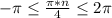 $-\pi \leq\frac{\pi*n}{4}\leq2\pi$, отсюда

    $-4 \leq\ n \leq 8$

Таким образом,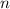 $n$ принимает значения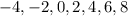 ${-4, -2, 0, 2, 4, 6, 8}$

Видно, что решения (3) уравнения составляют арифметическую прогрессию с первым членом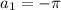 $a_{1}=-\pi$ и последним седьмым членом

 $a_{7}=\frac{8*\pi}{4}=2\pi$ 

Теперь мы можем найти сумму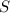 $S$ всех решений уравнения как сумму первых семи членов арифметической прогрессии: 

$S=7*\frac{a_{1}+a_{7}}{2}=7*\frac{-\pi+2\pi}{2}=3,5*\pi$