6
Объяснение:
Ограничения:
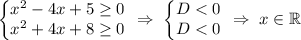

Замечаем, что первые два слагаемых имеют общую структуру в виде функции:
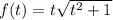
Действительно, если вместо t подставить x-2, то
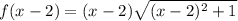
Аналогично
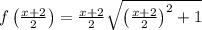
Тогда 3-е слагаемое нашего уравнения представим в виде разности двух линейных функций вида: g(t)=at
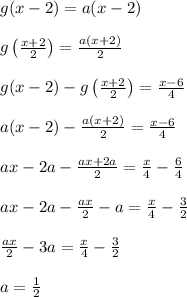
Дополним g(t) к основной функции:
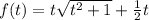
Исследуем ее на монотонность с производной
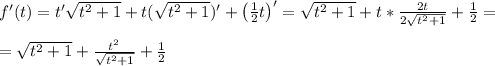
Заметим, что t²≥0; √(t²+1)>0, при любых действительных t, тогда
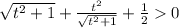
Значит f'(t)>0, следовательно f(t) - монотонно возрастающая функция на всей числовой оси
Для монотонных функций справедливо:
f(a)=f(b) ⇔ a=b
Перепишем наше уравнение в следующем виде
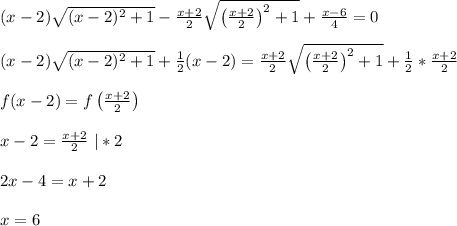
Ее сумма:
Sn = n(a1 + an)/2,
где а1 - первый член прогрессии, аn - последний член.
По условию а1=1, а поскольку все следующие числа представляют собой последовательно идущие числа, то последний член прогрессии совпадает с его номером n. Сумма должна быть меньше 528.
Получается неравенство:
528 > n(1+n)/2
n(1+n) < 1056
n^2 + n - 1056 <0
Найдем корни:
Дискриминант:
Корень из (1+4•1056) =
= корень из (1+4224) =
= корень из 4225 = 65
n1 = (-1+65)/2 = 64/2 = 32
n2 = (-1-65)/2 = -66/2 = -33 не подходит, поскольку корень не является натуральным числом.
(n-32)(n+32) <0
n-32<0
n+32>0
n<32
n>-32 - не подходит, поскольку n >0
1 < n < 32
Это значит, что n= 31.
ответ: 31
Проверка:
Если бы n=32, то:
(1+32)•32/2 = 33•32/2 = 33•16 = 528, значит сумма последовательных чисел от 1 до 32 была бы равна 528.