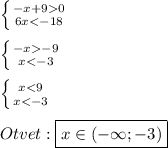
посмотрим на левую и правую части
правая часть минимум при x=0 принимает значение 2
берем производную (x^2+2)' = 2x = 0 х=0
левая максимум при х=0 и принимает значение 2
тоже ищем экстремумы 1-x>=0 x<=1
x+1>=0 x>=-1
ОДЗ -1 <= x <=1
ищем экстремумы на границах
при х=-1 выражение =√(1-(-1)) + √(1-1) = √2
при х=1 выражение = √(1-1) + √(1+1) = √2
(√(1+х) + √(1-х))' = 1/2√(1+x) - 1/2√(1-x) = (√(1-x) - √(1+x))/2√(1-x)√(1+x)=0
√(1-x) = √(1+x)
2x = 0
x=0
√(1-0) + √(1+0) = 2
максимум при х=0
значит решение х=0
======
ну можно сделать замену
1-x=u
1+x=t
и решать систему
u+t=2
√u + √t = u² + t²
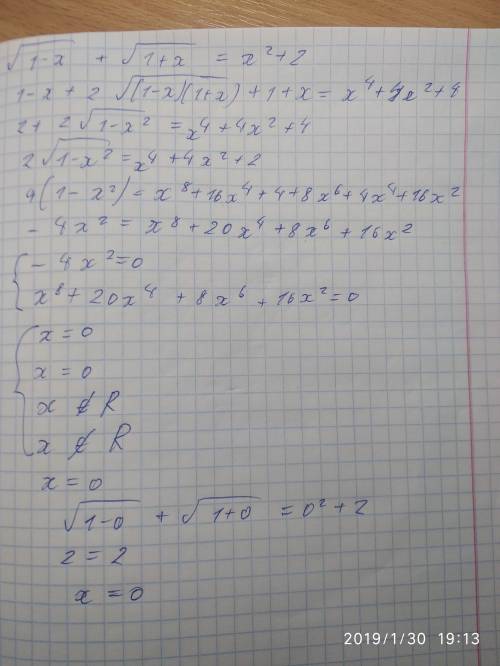 " />
" />
1). 4 по 10; 2 по 9; 4 по 8 40+18+32 = 90 - 10 выстрелов
3 по 10; 4 по 9; 3 по 8 30+36+24 = 90 - 10 выстрелов
2 по 10; 6 по 9; 2 по 8 20+54+16 = 90 - 10 выстрелов
1 по 10; 8 по 9; 1 по 8 10+72+8 = 90 - 10 выстрелов
Так как 90 - четное, то сумма попаданий по 9 очков должна быть четной.
Таких чисел существует четыре: 2; 4; 6; 8.
0 и 10 не могут быть по условию.
2). 4(3x² + x)² - 17(3x² + x) + 4 = 0
Заменим 3x² + x на у:
4y² - 17y + 4 = 0 D = b²-4ac = 289 - 64 = 225 = 15²
y₁ = (-b+√D)/2a = (17+15):8 = 4
y₂ = (-b -√D)/2a= (17-15):8 = 0,25
3x² + x - 4 = 0 D = b²-4ac = 1+48 = 49
x₁ = (-b+√D)/2a = (-1+7):6 = 1
x₂ = (-b -√D)/2a = (-1-7):6 = -4/3
3x² + x - 0,25 = 0
12x² + 4x - 1 = 0 D = b²-4ac = 16+48 = 64
x₃ = (-b+√D)/2a = (-4+8):24 = 1/6
x₄ = (-b -√D)/2a = (-4-8):24 = -1/2
ответ: {1; -4/3}, {1/6; -1/2}