11х - 4у = 21
Объяснение:
Так как прямая y=kx+b проходит через обе данные точки, что составим систему уравнений с неизвестными k и b, подставив, вместо х и у, координаты данных точек:
{3=3k+b,
{14=7k+b
и решим её
вычтем из нижнего уравнения верхнее, получим:
14-3 = 7k - 3k + b-b
11 = 4k
k = 11/4
подставим значение k в любое уравнение системы, получим:
3 = 3 * 11/4 +b
3 = 33/4 +b
b = 3 - 33/4
b = 3 - 8_1/4
b = -5_1/4
уравнение прямой имеет вид:
у = 11/4 х -5_1/4
у = 11/4 х - 21/4 | * 4 домножим всё на 4 (для более приличного вида)
4у = 11х - 21 , запишем иначе
11х - 4у = 21 - уравнение прямой проходящей через данные точки А и В
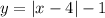
Область определения D(y): |R все числа, т.к. на х нет никаких ограничений.
Область значений E(x): [-1;+∞) т.к. минимальное значение модуля 0, то есть у=0-1=-1, и этот модуль ни чего не ограничивает сверху.
Есть функция y=|x| это 2 прямые, которые наклонены на 45° и 135° от оси Ох они имеют одну общую точку (0;0) и область значений [0;+∞) см. внизу.
Функция, которую надо построить сдвинута на 4 вправо т.к. |x-4| или f(x-4) и поднята на -1 т.к. y=f(x)-1. Исследуя полученный график видно, что функция лежит в 1,2 и 4 четверти, но при желании можно раскрыть модуль по определению и исследовать каждую прямую отдельно и узнать другим в каких четвертях.
zₓ'=((x+2y)*y²)ₓ'=(xy²+2y³)ₓ'=(xy²)ₓ'+(2y³)ₓ'=y²+0=y²
Частная производная по у (при переписывании вместо а надо писать у, в предложенных индексах нет такой буквы, потому использую а:
zₐ'=((x+2y)*y²)ₐ'=(xy²+2y³)ₐ'=(xy²)ₐ'+(2y³)ₐ'=2xy+6y²
в) zₓ'=(9(x-y²)⁴)ₓ'=9*((x-y²)⁴)ₓ'*(x-y²)ₓ'=9*4*(x-y²)³*1=36(x-y²)³
zₐ'=((9(x-y²)⁴)ₐ'=9*((x-y²)⁴)ₐ'*(x-y²)ₐ'=9*4*(x-y²)³*(-2y)=-72y(x-y²)³
б) zₓ'=(cos(2x+e^y))ₓ'=(cos(2x+e^y))ₓ'*(2x+e^y)ₓ'=-sin(2x+e^y)*2=-2sin(2x+e^y)
zₐ'=(cos(2x+e^y))ₐ'=(cos(2x+e^y)ₐ'*(2x+e^y)ₐ'=-sin(2x+e^y)*e^y