Раз наш участок можно будет огородить забором в 300 метров, то его периметр не должен превышать 300.
Пусть  и
и  - две стороны нашего участка, тогда
- две стороны нашего участка, тогда 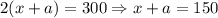 .
.
Площадь прямоугольника - произведение двух смежных его сторон.
Составим функцию площади нашего участка в зависимости, например, от стороны  .
.
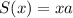
Но 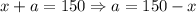 , следовательно, наша функция принимает вид
, следовательно, наша функция принимает вид
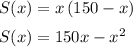
С производной найдём экстремум данной функции.
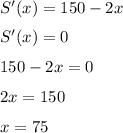
Т.к. исходная функция - парабола с опущенными вниз ветвями, то данная точка - максимум функции. Следовательно, при условии периметра в 300 метров, для достижения наибольшей площади участка одна из сторон должна быть равна 75 метров, значит, другая сторона также должна быть 75 метров (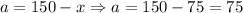 ).
).
Получаем максимальную площадь 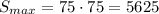 квадратных метров.
квадратных метров.
ответ. 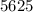 кв. м.
кв. м.
Пусть радиус окружности равен 1 (это скорее всего и имелось ввиду в задании). Тогда абсцисса точки на окружности это косинус угла φ рад. и соответствующего ему числа φ, где φ рад. - такой угол, на который повернут радиус-вектор точки из положения с координатами (1, 0)
Короче, что толку сыпать теорией, главное в вышесказанном, то что y - синус угла, а х - косинус. Нам нужно найти подходящие точки, а значит и соотвествующие им углы.
Тогда
1)
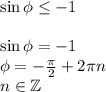
2)

Таких чисел/углов и соотвествующих им точек не существует.
3)
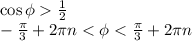
1) x:2+5=10
x:2=10-5
x:2=5
x=5*2
x=10
2)−3,1⋅x+5,4=−2,35
-3,1x=-2,35-5,4
-3,1x=-7,75
x=7,75:3,1
x=2,5
3)7(3y+11)=−9(4y−5)+2y−7
21y+77=-36у+45+2у-7
21у+34у=38-77
55у=-39
у=-39/55
4)2(5s+11)−3(4s+5)+7(2s−6)=10s−20
10s+22-12s-15+14s-42=10s-20
2s=-20+35
2s=15
s=7,5
5)2,5(1 1/3*z+0,2)= −0,4z+ 1 1/4
2,5(4z/3+0.2)=-0.4z+1.25
10/3z+0.5=-0.4z+1.25
10/3z+0.4z=1.25-0.5
56/15z=0.75
z=3/4*15/56
z=45/224
6)1/4(1,2y+2,2)−3(1,5y− 1/3)+2(y−1,9)−y+1=0
0,25*(1,2y+2,2)-4,5y+1+2y-3,8-y+1=0
0,3y+0,55-3,5y-1,8=0
-3,2y=1,25
y=-25/64