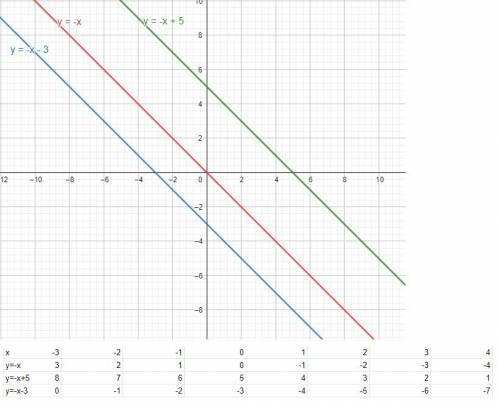
прямая проходящяя через точку (0;0) - начало координат
на 5 единиц
y=-x+5 есть прямая, параллельная графику прямо пропорциональной зависимости y=-x
в 5 единицах от начала координат, то есть в точке с координатами (0;5)
на 3 единицы вниз
есть прямая
зависимости y=-x
в /-3/ единицах от начала координат, то есть в точке с координатами (0; -3)
вывод:
является прямая
зависимости y = ax
в точке с координатами (0; b)
на b единиц от начала координат
на |b| единиц от начала координат
достаточно знать координаты одной точки
потому что другая точка пересекает ось Oy в координатах (0; b)
4 (x-y)=-2,
{ 3x-7y=-2,5-2(x+y);
1) Поработаем со вторым уравнением, упростим его.
3x-7y=-2,5-2(x+y)
3x-7y=-2,5-2x-2y
Перенесем выражения с переменными в левую сторону, свободные члены в правую.
3x-7y+2x+2y=-2,5
5x-5y=-2,5 |:5 (поделим все уравнение на пять)
x-y=-0.5
2. Запишем получившуюся систему:
{4 (x-y)=-2
{x-y=-0.5
Раскроем скобки в первом уравнении, получим:
{4x- 4y=-2
{x-y=-0.5
3. Выразим из второго уравнения x.
x-y=-0.5
x=y-0.5
4. Подставим получившийся х в первое уравнение:
4*(у-0.5)-4у=-2
4у-2-4у=-2
лайк
Объяснение: