3/(2^(2 - x²) -1)² - 4/(2^(2- x²) -1) + 1 ≥ 0 ;
замена : t = 2^(2-x²) -1
3 / t² - 4 / t +1 ≥ 0 ;
(t² - 4t +3) / t² ≥ 0
для квадратного трехчлена t² - 4t +3 t₁=1 корень: 1² - 4*1+3 = 1- 4+3 =0.
t₂ =3/t₁=3/1=1 (или t₂ =4 -1=3)
* * * наконец можно и решить уравнение t² - 4t +3=0 * * *
(t² - 4t +3) / t² ≥ 0 ⇔ (t -1)(t - 3) / t² ≥ 0 .
+ + - +
Объяснение:a)
{ 2^(2-x²) -1 ≤ 1 ; 2^(2-x²) -1 ≠ 0 .⇔ { 2^(2-x²) ≤ 2 ; 2^(2-x²) ≠ 1 . ⇔
{ 2^(2-x²) ≤ 2¹ ; 2^(2-x²) ≠ 2⁰.⇔ {2-x² ≤ 1 ; 2 - x² ≠ 0.⇔{ x² -1 ≥ 0 ; x² ≠ 2⇔
{ (x+1)(x-1) ≥ 0 ; x ≠ ±√2 . ⇒ x∈ ( -∞ ; -√2 ) ∪ (-√2 ; -1] ∪ [1 ; √2) U (√2 ; ∞) .
b)
2^(2-x²) -1 ≥ 3 ⇔ 2^(2-x²) ≥ 4 ⇔2^(2-x²) ≥ 2² ⇔2- x² ≥ 2 ⇔ x² ≤ 0 ⇒ x=0.
ответ: x∈ ( -∞ ; -√2 ) ∪ (-√2 ; -1] ∪ { 0} ∪ [1 ; √2) U (√2 ; ∞) .
Объяснение:
1. D=1^2-4*1*1=1-4= -3 D меньше 0, следовательно, решений нет!
ответ: корней нет
2. D=7^2-4*10=49-40=9
x1, x2= (7+-3)/2=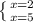
ответ: 2; 5
3. 6x^2-5x+1=0
D=25-4*6=1
x1, x2=(5+-1)/12=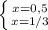
ответ: 1/3; 0,5
4. D=49-4*12=1
x1, x2=(-7+-1)/12=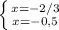
ответ: -2/3; -0,5
5. Заменим X^2=t
t^2-5t+4=0
D=25-4*4=9
x1, x2=(5+-3)/2=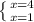
Вернемся к замене
x^2=1 или x^2=4
ответ: -2; -1; 1; 2