1. ОДЗ: х ∈ R
2. Функция не является четной или нечетной, то есть общего вида.
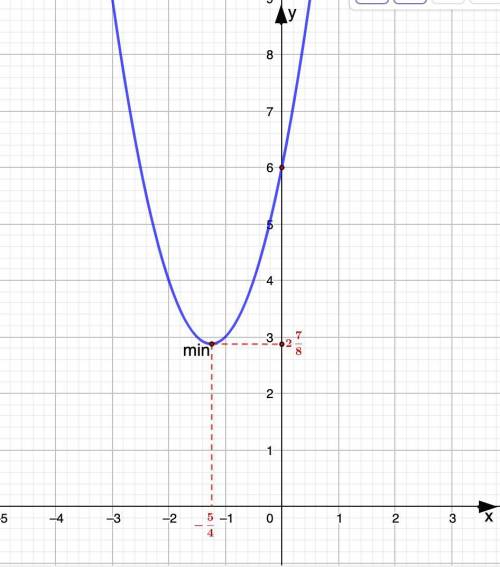
3. х = 0 ⇒ у = 6
ось 0х не пересекает
4. Асимптот нет
5. Функция убывает на промежутке (-∞; -5/4]
Функция возрастает на промежутке [-5/4; +∞)
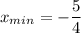
6. Функция вогнута.
Объяснение:
Требуется исследовать функцию и построить график.
y = 2x² + 5x + 6
1. ОДЗ: х ∈ R
2. Четность, нечетность.
Если f(-x) = f(x), функция четная.
Если f(-x) = -f(x), функция нечетная.
у(-х) = 2 · (-х)² + 5 · (-х) + 6 = 2х² - 5х + 6
у(-х) ≠ у(х) ≠ -у(х) ⇒ функция не является четной или нечетной, то есть общего вида.
3. Пересечение с осями:
1) х = 0 ⇒ у = 6.
Ось 0у график пересекает в точке (0; 6)
2) у = 0 ⇒ 2х² + 5х + 6 = 0
D = 25 - 4 ·2 · 6 = - 23 <0
⇒ корней нет, ось 0х не пересекает.
4. Асимптоты.
Функция непрерывна, асимптот нет.
5. Возрастание, убывание, экстремумы.
Найдем производную:
y' = 2 · 2x + 5 = 4x + 5
Приравняем к нулю и найдем корни:
4х + 5 = 0
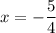
Отметим точку на числовой оси и определим знак производной на промежутках:
![\displaystyle [-\frac{5}{4} ]](/tpl/images/4839/7141/129a0.png)
⇒ Функция убывает на промежутке (-∞; -5/4]
Функция возрастает на промежутке [-5/4; +∞)
Если производная меняет знак с минуса на плюс, то в данной точке будет минимум.
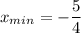
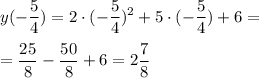
⇒ координаты точки минимума (-5/4; 2 7/8)
6. Выпуклость, вогнутость, точки перегиба.
Найдем производную второго порядка:
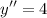
y'' > 0
Если вторая производная больше нуля, то функция вогнута.
Точек перегиба нет.
Строим график.
А ещё я люблю этого автора за афористичность, за умение его в одной фразе сконцентрировать суть истины, которую порой трудно объяснить доходчиво:
Человек непонятлив, когда речь идет о том, на что ему наплевать.
Чтобы уйти от человека, надо иногда придумывать ложные причины. Потому что истинные бывают слишком жестоки. Но чтобы ПРИЙТИ, ничего не нужно придумывать. Надо просто прийти, и все.
Беспечное счастье выглядит жестоким и наглым, потому что еще далеко не все люди на свете счастливы.
И что бы там ни говорили, если я плачу над повестью "В тылу как в тылу" , долго размышляю о "Позднем ребёнке", перечитываю "Безумную Евдокию"... значит для меня это хорошие книги и хороший писатель".