Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
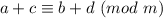
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
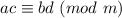
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
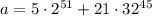
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 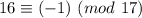 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 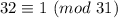 , получаем
, получаем
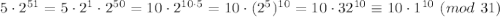
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
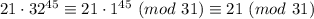
Остаток 21, чудесно. Выполняем последний шаг.
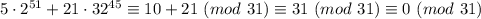
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
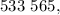 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).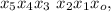


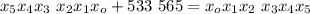 ;
;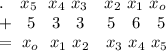

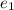 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого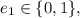
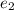 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго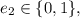
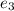 – возможная добавочная единица,
– возможная добавочная единица,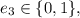
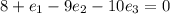 ;
;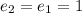 и при
и при  ;
;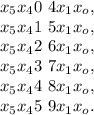
 поскольку
поскольку 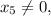 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.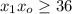 .
.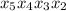 .
.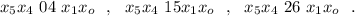
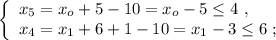

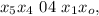
 может играть роль апреля.
может играть роль апреля.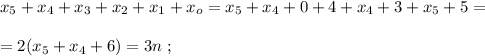
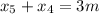 ;
;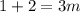 ;
;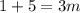 ;
;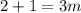 ;
; ;
;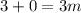 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.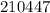 – дата 21/04/47 г.
– дата 21/04/47 г.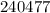 – дата 24/04/77 г.
– дата 24/04/77 г.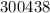 – дата 24/04/38 г.
– дата 24/04/38 г.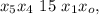
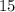 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;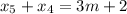 ;
;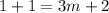 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

Обозначим A = {-3, -1, 1, 2, 7, 9}. Множество A состоит из 6-и элементов. Обозначим отношение "х принадлежит множеству X = {a, b, c, ...}" как x in X = {a, b, c, ...}.
а) Общее количество точек N равно числу пар (x,y) таких, что: (x,y) in AxA, или, другими словами, (x,y): x in X = {-3, -1, 1, 2, 7, 9}, и y in Y = {-3, -1, 1, 2, 7, 9} => N = 6x6 = 36 (т.к. x можно выбрать из X 6-ю и каждому такому выбору соответвует 6 значений y из Y).
б) Наши пары должны быть парами вида (x,y): x < 0, y > 0 => x in X = {-3, -1}, а y in Y = {1, 2, 7, 9}. Всего можно составить 2*4 = 8 таких пар (x,y). Следовательно, 8 точек лежит во второй координатной четверти.
в) Рассуждаем аналогично (б). Составляем пары вида (x,y): x > 0, y < 0 => x in X = {1, 2, 7, 9}, а y in Y = {-3, -1} => Всего таких пар (x,y) можно составить 4*2 = 8. . Следовательно, 8 точек лежит в четвертой координатной четверти.
г) Составляем пары вида (x,y): x^2 + y^2 ≤ r^2 = 5^2 => (x,y): (-3,-3), (-3,-1), (-3,1), (-3,2), (-1,-3), (-1,-1), (-1,1), (-1,2), (1,-3), (1,-1), (1,1), (1,2), (2,-3), (2,-1), (2,1), (2,2). Как видим, всего существует 16 таких пар (x,y). Следовательно, в круге радиусом 5 с центром в начале координат лежат 16 точек.