вот решение м
Объяснение:
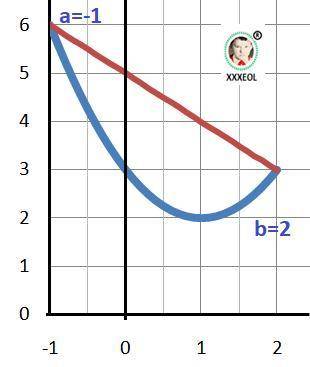
Дано: F(x) = x² -2*x + 3, y(x)= -x+5
Найти: S=? - площадь фигуры
1) Находим точки пересечения графиков: F(x)=y(x).
-x²+x+2=0 - квадратное уравнение
b = - верхний предел, a = - 1 - нижний предел.
2) Площадь - интеграл разности функций. Прямая выше параболы.
s(x) = y(x) - F(x) = -2 -x + x² - подинтегральная функция
3) Интегрируем функцию и получаем:
S(x) = -2*x -1/2*x² + 1/3*x³
4) Вычисляем на границах интегрирования.
S(b) = S(2) = -4 -2 + 2,67 = -3,33
S(a) = S(-1) = 2 -0,5 -0,33 = 1,17
S = S(-1)- S(2) = 4,5(ед.²) - площадь - ответ
Рисунок к задаче в приложении.
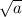. Эта система будет иметь единственное решение только тогда, когда эти окружности касаются. Они могут касаться внешним или внутренним образом. Наименьшее значение 
будет при внешнем касании, когда сумма радиусов равна расстоянию между центрами. Расстояние между центрами равно 
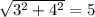. Значит, искомое получится из условия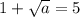 
, т.е. a=16. ответ: Б.
вот надо у выражения с x