Для начала упростим имеющееся выражение по формуле произведения синуса на косинус:
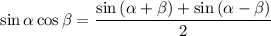
В нашем случае получается:

Итак, от 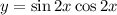 мы перешли к
мы перешли к  . Теперь будем рассматривать период. Говоря простым языком, период - это какое-то определённое значение, пройдя которое мы вернёмся в ту же самую точку, из которой начинали движение. Должно выполняться вот это равенство:
. Теперь будем рассматривать период. Говоря простым языком, период - это какое-то определённое значение, пройдя которое мы вернёмся в ту же самую точку, из которой начинали движение. Должно выполняться вот это равенство: 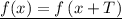 , где
, где 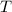 - это и есть этот период. В нашем случае получается вот так:
- это и есть этот период. В нашем случае получается вот так:

Теперь есть два решения этого уравнения. Первый - это муторный и прямолинейный. Просто перенести всё в левую часть, далее через разность синусов и так медленно добираться до периода. Второй намного проще, но надо понимать, что происходит. Дело в том, что 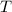 мы изменять не можем, так как это переменная, которую нам надо найти. Зато
мы изменять не можем, так как это переменная, которую нам надо найти. Зато  мы можем присвоить любое удобное нам значение. Он ни на что не влияет, равенство в рамке продолжает соблюдаться, поскольку мы заменим икс в обеих частях, но всё станет намного проще. Например, здесь удобнее взять
мы можем присвоить любое удобное нам значение. Он ни на что не влияет, равенство в рамке продолжает соблюдаться, поскольку мы заменим икс в обеих частях, но всё станет намного проще. Например, здесь удобнее взять  . Нам известно, что
. Нам известно, что  , и вся левая часть в него превратится. Получится вот так:
, и вся левая часть в него превратится. Получится вот так:
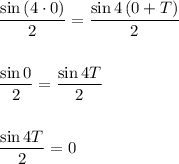
Теперь просто решаем обычное тригонометрическое уравнение и находим 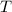 .
.
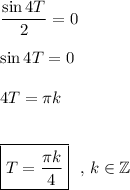
Итак, вот мы к этому и пришли. Возникает вопрос, что делать с 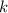 ? В условии задания написано, что нужно найти наименьший положительный период данной функции. Так как
? В условии задания написано, что нужно найти наименьший положительный период данной функции. Так как 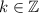 , то
, то 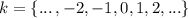 . Положительное число должно быть больше нуля, и очевидно, что
. Положительное число должно быть больше нуля, и очевидно, что 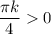 при
при  . Поэтому подставляем наше первое значение:
. Поэтому подставляем наше первое значение: 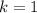 . При нём получаем:
. При нём получаем:
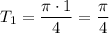
Но не стоит сразу радоваться. Сначала проверим период на соответствие равенству  .
.
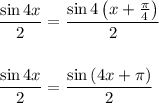
Согласно формуле приведения, 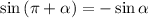 , отсюда имеем:
, отсюда имеем:
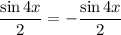
Равенство не выполнено, значит, 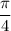 не является периодом данной функции. Проверяем дальше,
не является периодом данной функции. Проверяем дальше, 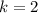 .
.

Точно так же подставляем в 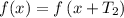 .
.
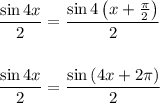
По формуле приведения 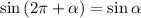 , поэтому:
, поэтому:
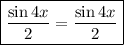
А потому 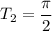 и является искомым периодом.
и является искомым периодом.
ответ: В)
b=-2x+y
Объяснение:
Hogyfoxgkofhf