1) Матрица линейного оператора выглядит следующим образом
α₁₁ α₁₂
α₂₁ α₂₂
Составим соответствующие уравнения после действия этого оператора
5α₁₁+4α₁₂=11
5α₂₁+4α₂₂=25
4α₁₁-3α₁₂=-16
4α₂₁-3α₂₂=-11
Решая систему находим элемениы матрицы
α₁₁=-1 α₁₂=4
α₂₁= 1 α₂₂=5
ответ: 9
2) Составим матрицу оператора
1 7 8
-5 -1 8
-2 -4 1
Транспонируем ее
1 -5 -2
7 -1 -4
8 8 1
ответ: 17
3) Решим соответствующее характеристическое уравнение
![\left[\begin{array}{cc}12-\lambda&24\\-6&38-\lambda\end{array}\right]=\lambda^2-50\lambda+600=0](/tpl/images/0065/8513/12cc7.png)
Для всех собственных значений найдем собственные вектора
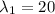
-x₁+3x₂=0
x₁=1 x₂=1/3
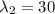
-3x₁+4x₂=0
x₁=1 x₂=3/4
ответ: 13/12
4) x₁²+4x₁x₂+4x₁x₃+29x₂²+38x₂x₃+17x₃²=(x₁+2x₂+2x₃)²+(5x₂+3x₃)²+4x₃²=a₁²+a₂²+4a³₂
ответ: 6
X<1, x<2
Объяснение:
1)2х<х+1, х<1
2)log2x<1, x<2^1, x<2
3)ТАК КАК 0.5 меньше нуля, решение будет вот таким: (1-х)<=(0.5)^(-1), 1-х<=2, х>=-1 (-1; до +бесконечности)
4) lg3x=lg(x+4), 3x=x+4, 2x=4, x=2
5)x^2-6x+19=10, x^2-6x+9=0, (x-3)^2=0, x-3=0, x=3
6)5+2x=0.3, 2x=-4.7, x=-4.7/2, x=-2.23