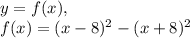
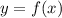— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 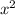(не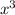 
, не 
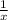, не 
и не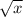 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид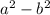 
, где 
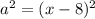, и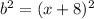 
. Формула «разность квадратов» раскрывается так: 
.
.
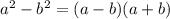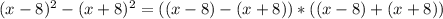
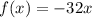, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
1. Диета: не больше 5-и тортиков в день:
2. Максимум может съесть 8 тортиков в день;
3. Условие, если 1 день - 8 тортиков,
то 2 следующих дня - по 3 тортика в день;
Если предположить, что с 01.12 до 31.12 сила воли слону не оказала ни разу, то слон съел бы за месяц (в декабре 31 день)
31*5=155 тортиков
Поскольку, по условию, сила воли иногда отказывает, то минимальное количество дней, когда слону отказала сила воли, = 1.
Если предположить, что слон съел максимальное количество тортиков, 8 шт, 31 декабря, то количество съеденного будет
30*5+8=158 тортиков, и диета - закончилась))
Если предположить, что день отказа силы воли пришелся не позже, чем 3 дня до конца декабря, то количество съеденных тортиков будет:
28*5+8+3+3=154 тортика
ответ: 158 тортиков
x∈[5;+∞)
Объяснение:
Реши неравенство и выбери правильный ответ:
3x−11≥−5x+29
3х+5х ≥29+11
8х ≥40
х≥5
x∈[5;+∞)
Неравенство нестрогое, 5 входит в число решений неравенства, скобка квадратная, а у знаков бесконечности скобка всегда круглая.
Варианты ответов:
x∈[5;+∞]
x∈[−5;+∞)
x∈(5;+∞)
x∈[5;+∞)
x∈(−∞;−5)