Как то так
Объяснение:
Всё смотри на фото
Обозначим все это через переменные:
х - количество коров на 2-й ферме
0,88 х - количество коров на 1-й ферме
теперь:
100% - молока дает каждая корова на 2-й ферме
100% + 7,5% = 107,5% - молока дает каждая корова на 1-ой ферме
у литров молока дает каждая корова на 2-й ферме
107,5% от у = у: 100% · 107,5% = 1,075 у литров молока дает каждая корова на 1-ой ферме.
Узнаем сколько молока получает каждая ферма.
1,075 у · 0,88 х = 0,946 ху л молока получает 1-ая ферма.
ху л молока получает 2-ая ферма.
Переводим в проценты:
ху = 100% молока получает вторая ферма, тогда
0,946 ху = 0,946·100% = 94,6% молока получает первая ферма.
Очевидно, что 2-я получает больше 1-й
100% - 94,6% = 5,4%
ответ: на 5,4% вторая 2-я получает больше первой.
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)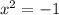 
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 
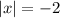
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)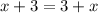 
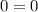
корней уравнения нет.
2) 
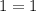
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: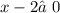 
, 
;
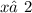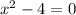
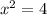
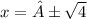
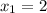(не удовлетворяет ОДЗ), 
ответ: 
2)
,
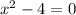
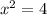
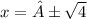
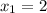ответ: ; 
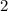
=> уравнения не равносильные.
10. 1)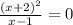 
ОДЗ: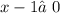 
, 
;
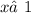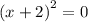
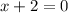
ответ:
2)
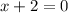
ответ:
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 
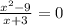
ОДЗ: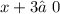 
, 
;
, 
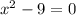
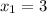(не удовлетворяет ОДЗ)
ответ: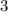 
13. 
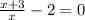
ОДЗ: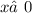 
;
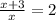
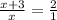
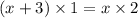
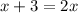
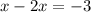
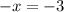
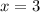
ответ: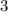
14. 
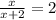
ОДЗ: 
, 
;
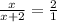
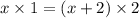
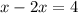
ответ: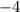 
15. 
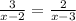
ОДЗ: , ,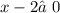 
, 
;
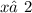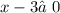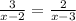
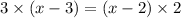
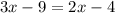
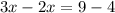
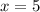
ответ: 
16. 
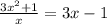
ОДЗ: ;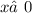
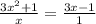
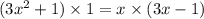
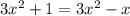
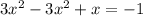
ответ: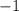 
fvevefvvevev
Объяснение: