3,75 км/ч.
Объяснение:
Пусть скорость туриста на подъёме равна x км/ч, тогда его скорость на спуске равна ( x + 0,6 ) км/ч. Если спуск занял 1,5 часа, то пройденное за это время расстояние составит ( x + 0,6 ) * 1,5 = 1,5x + 0,9 км.
Если весь путь занял 2 часа, а спуск - 1,5 часа, то подъём занял 2 - 1,5 = 0,5 часа. За это время турист (двигаясь со скоростью x км/ч) 0,5 * x = 0,5x км.
Учитывая, что весь путь равен 7,2 км, можно составить уравнение:
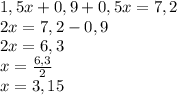
Скорость на подъёме составила 3,15 км/ч, следовательно скорость на спуске равна 3,15 + 0,6 = 3,75 км/ч.
КЛАССИФИКАЦИЯ: Линейное неоднородное дифференциальное уравнение второго порядка со специальной право частью
Найти нужно: yо.н. = уо.о. + уч.н.
Найдем уо.о. (общее однородное)
Применим метод Эйлера
Пусть
Корни которого
Тогда общее решение однородного уравнения будет
Найдем теперь уч.н.(частное неоднородное)
где
Сравнивая
уч.н. =
Чтобы определить коэффициенты А и В, воспользуемся методом неопределённых коэффициентов:
Подставим в исходное уравнение и приравниваем коэффициенты при одинаковых х
Тогда частное решение неоднородного будет иметь вид
уч.н.
Запишем общее решение исходного уравнения