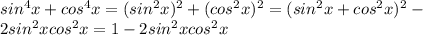
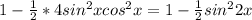
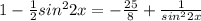
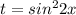Алгебра: Постройте график уравнения ( х-1)2 + у2 = 4

1) х=2, у=1. 2) х=2, у=-23) х=2, у=14) х=2, у=3№2. х=-2, у=3. Объяснение:№1. Суть метода подстановки заключается в том, что ты выражаешь одну из переменных из одной строки (то есть приводишь строку к виду х = ...) и подставляешь это ... вместо х во вторую строку. 1) Выразим х из первой строки. Для этого перенесём 2у в правую сторону:Теперь заменим х во второй строке на (4 - 2у) (т.к. х = 4 - 2у):Раскроем скобки во второй строке::Решим уравнение во второй строке:Теперь мы знаем, что y = 1. Подставим...

Постройте график уравнения ( х-1)2 + у2 = 4

👇

Увидеть ответ

Ответ:

EgorJORDAN

17.01.2021

х2-2=4

х2=4+2

х2=6

х=3

ж:3

4,6(24 оценок)

Открыть все ответы

Ответ:

даун47

17.01.2021

Преобразуем левую часть:
$sin^{4} x + cos^{4} x = ( sin^{2}x) ^{2} + (cos^{2}x) ^{2} = ( sin^{2}x + cos^{2}x) ^{2} - \\ 2 sin^{2} x cos^{2} x = 1 - 2 sin^{2} x cos^{2} x$

Далее:
$1 - \frac{1}{2} * 4 sin^{2} x cos^{2}x = 1 - \frac{1}{2} sin^{2} 2x$
Таким образом, получаем уравнение:
$1 - \frac{1}{2} sin^{2}2x = -\frac{25}{8} + \frac{1}{ sin^{2}2x }$
Теперь понятно, что можно ввести замену $t = sin^{2}2x$ и продолжать решение уже дробно-рационального уравнения.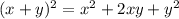

Советую запомнить приём, который я здесь употребил. Он состоит вот в чём.
Мы помним формулу сокращённого умножения:
$(x+y)^{2} = x^{2} + 2xy + y^{2}$
Отсюда я могу легко выразить сумму квадратов:
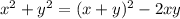
$x^{2} + y^{2} = (x+y)^{2} - 2xy$
Думаю, Вы уже догадались, что в нашем уравнении сыграло роль x, а что y.
Этот приём встречается очень часто в самых неожиданных ситуациях, так что рекомендую запомнить его.
Уравнение можно было решить и по формулам понижения степени(правда, это значительно было бы сложнее). Но в целом, можно рассмотреть и такой вариант, но я показал проще.

Делаем замену:
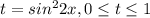
$t = sin^{2} 2x, 0 \leq t \leq 1$
После замены получаем:
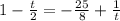
$1 - \frac{t}{2} = - \frac{25}{8} + \frac{1}{t}$
Умножаем обе части уравнения на 8t(с дробями работать крайне неудобно, да и t в знаменателе нам ни к чему - просто запомним, что он должен быть отличным от 0, а потом проверим это):
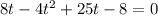
$8t - 4 t^{2} + 25t - 8 = 0$
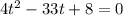
$4 t^{2} - 33t + 8 = 0$
Решаем квадратное уравнение(кстати, t уже отличен от 0. В этом можно убедиться прямой подстановкой)
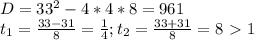$D = 33^{2} - 4 * 4 * 8 = 961 \\ 
 t_{1} = \frac{33 - 31}{8} = \frac{1}{4}; t_{2} = \frac{33 + 31}{8} = 8 \ \textgreater \ 1$ - этот корень не удовлетворяет нашему уравнению.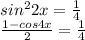
Следовательно, возвращаясь к переменной x, получаем простейшее уравнение:
$sin^{2} 2x = \frac{1}{4} \\ \frac{1 - cos 4x}{2} = \frac{1}{4}$
Отсюда
$cos 4x = \frac{1}{2} \\ 4x = +- \frac{ \pi }{3} + 2 \pi n \\ x = +- \frac{ \pi }{12} + \frac{ \pi n}{2}$
Это и есть ответ. Напомню, что при решении простейшего уравнения я использовал формулу понижения степени, а в конечном результате n - целое число.

4,7(25 оценок)

Ответ:

elizalove21345747

17.01.2021

1) х=2, у=1.

2) х=2, у=-2

3) х=2, у=1

4) х=2, у=3

№2.

х=-2, у=3.

Объяснение:

№1.

Суть метода подстановки заключается в том, что ты выражаешь одну из переменных из одной строки (то есть приводишь строку к виду х = ...) и подставляешь это ... вместо х во вторую строку.

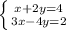
1) $\left \{ {{x + 2y=4} \atop {3x-4y=2}} \right.$

Выразим х из первой строки. Для этого перенесём 2у в правую сторону:

$\left \{ {{x=4-2y} \atop {3x - 4y = 2}} \right.$

Теперь заменим х во второй строке на (4 - 2у) (т.к. х = 4 - 2у):

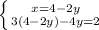
$\left \{ {{x=4-2y} \atop {3(4-2y) - 4y = 2}} \right.$

Раскроем скобки во второй строке:

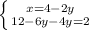
: $\left \{ {{x=4-2y} \atop {12-6y-4y=2}} \right.$

Решим уравнение во второй строке:

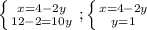
$\left \{ {{x=4-2y} \atop {12-2 = 10y}} \right. ; \left \{ {{x=4-2y} \atop {y=1}} \right.$

Теперь мы знаем, что y = 1. Подставим 1 вместо у в уравнение из первой строчки:

x = 4 - 2*1

x = 2.

Проверка:

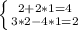
$\left \{ {{2 + 2*1 = 4} \atop {3*2 - 4*1 = 2}} \right.$

ответ: x=2; y = 1.

Таким же решим другие системы:

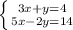
$\left \{ {{3x + y = 4} \atop {5x - 2y = 14}} \right.$

В этом случае удобнее выразить из первой строчки у (вообще обычно выражают ту переменную, перед которой нет коэффициента):

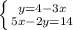
$\left \{ {{y=4 - 3x} \atop {5x - 2y = 14}} \right.$

Подставим (4 - 3x) вместо у во вторую строку:

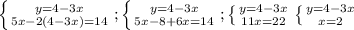
$\left \{ {{y=4 - 3x} \atop {5x - 2(4-3x) = 14}} \right. ; \left \{ {{y=4 - 3x} \atop {5x - 8 + 6x = 14 }} \right. ; \left \{ {{y=4 - 3x} \atop {11x = 22}} \right. \left \{ {{y=4-3x} \atop {x = 2}} \right.$

Теперь подставим 2 вместо х в первую строку:

у = 4 - 3*2 = 4 - 6 = -2.

Проверка:

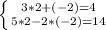
$\left \{ {{3*2 + (-2) = 4} \atop {5*2 -2*(-2) = 14}} \right.$

ответ: х = 2, у = -2.

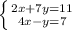
$\left \{ {{2x+7y=11} \atop {4x-y=7}} \right.$

Здесь выразим у из второй строки:

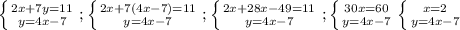
$\left \{ {{2x+7y=11} \atop {y=4x-7}} \right. ; \left \{ {{2x+7(4x-7)=11} \atop {y=4x-7}} \right. ;\left \{ {{2x+28x-49=11} \atop {y=4x-7}} \right.; \left \{ {{30x=60} \atop {y=4x-7}} \right. \left \{ {{x=2} \atop {y=4x-7}} \right.$

Подставим 2 вместо х во вторую строку:

у = 4*2-7 = 1

Проверка:

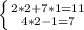
$\left \{ {{2*2 + 7*1 = 11} \atop {4*2-1=7}} \right.$

ответ: х=2, у=1.

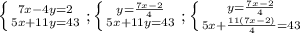
$\left \{ {{7x-4y=2} \atop {5x+11y=43}} \right. ; \left \{ {{y=\frac{7x - 2}{4} } \atop {5x+11y=43}} \right. ; \left \{ {{y=\frac{7x-2}{4} } \atop {5x+\frac{11(7x-2)}{4}=43 }} \right.$

Домножим обе части второго уравнения на 4:

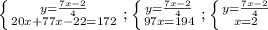
$\left \{ {{y=\frac{7x-2}{4} } \atop {20x + 77x-22 = 172}} \right. ; \left \{ {{y=\frac{7x-2}{4} } \atop {97x=194}} \right. ; \left \{ {{y=\frac{7x-2}{4} } \atop {x=2}} \right.$

Подставим 2 вместо х в первое уравнение:

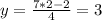
$y= \frac{7*2-2}{4} = 3$

Проверка:

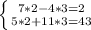
$\left \{ {{7*2 - 4*3 = 2} \atop {5*2+11*3=43}} \right.$

ответ: х=2, y=3.

№2.

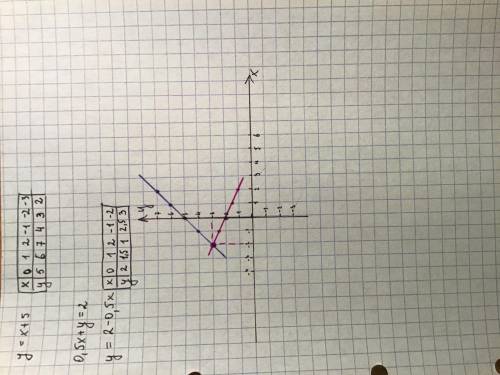
Чтобы графически решить систему уравнений, нужно построить график функции по каждому из уравнений системы. Координаты точки пересечения графиков — корни системы.

Решение см. на рисунке (прикреплён). Синий график — для y = x + 5, фиолетовый — для 0,5x + 6 = 2.

По рисунку видно, что точка пересечения графиков имеет по оси х координату -2, а по оси у — координату 3.

ответ: х=-2; у=3.