Чтобы доказать, что треуг равноб, нужно найти длины всех трех сторон: координаты стороны АВ (из конца вычитаем начало) : (2-(-6); 4-1)=(8;-3) АВ= корень квадратный из (восемь в квадрате плюс (минус три в квадрате) = корень квадратный из семидесяти трех аналогично все остальные стороны ВС=(2-2;-2-4)=(0;-6) длина ВС = корень квадратный из (ноль в квадрате плюс (минус шесть в квадрате)) = корень из 36 = 6 АС=(2-(-6);-2-1)=(8;-3) АС=корень квадратный из суммы квадратов координат получаем, что и длина АС равна корень из 75 АВ=АС, то есть треуг равноб
Решение: Обозначим собственную скорость моторной лодки за (х) км/час, тогда скорость лодки по течению равна: (х+2) км/час а против течения реки (х-2) км/час Расстояние пройденной лодкой по течению равно: S=V*t или: S=(х+2)*4 (км) Расстояние пройденной лодкой против течения равно: S=(x-2)*2 (км) А так как по течению моторная лодка на 28 км больше чем против течению, составим уравнение: (х+2)*4 - (х-2)*2=28 4х+8-2х+4=28 2х=28-12 2х=16 х=16:2 х=8 (км/час- собственная скорость моторной лодки)
ответ: Собственная скорость моторной лодки 8км/час
Объяснение:
°- вместо штриха
1) 2*2x=4x (табличные производные)
2) 3*4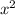 (табличные производные)
(табличные производные)
3) По правилу нахождения производной от умножения
(х³+6х−3)° * (x+1) + (х³+6х−3) * (x+1)°= (3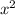 +6) * (x+1) + (х³+6х−3)* 1=
+6) * (x+1) + (х³+6х−3)* 1=
3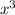 +3
+3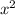 +6x +6 + х³+6х−3 =4
+6x +6 + х³+6х−3 =4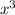 +3
+3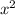 +12x +3
+12x +3
4) По правилу нахождения производной от деления
(4х-7)° * (х²+4) -(4х-7)* (х²+4)° / (х²+4)^2 =
4(х²+4)- 2x(4х-7) / (х²+4)^2 =
4х²+16 -8х² -14x / (х²+4)^2 =
-4х² -14x +16 / (х²+4)^2