
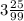
Объяснение:
3,(25)
Чтобы обратить периодическую дробь в обыкновенную достаточно записать в числителе период , а в знаменателе записать стольно девяток, сколько цифр в периоде
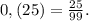
Значит
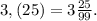
Обозначим данное число через x
x=3,(25) = 3,252525... .(1)
Умножим обе части данного равенства на 100
100x = 325,252525... .(2)
Вычтем почлено из уравнения (2 ) уравнение (1), получим
99x= 322;
x=322:99;
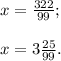
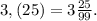
Представим данное число в виде суммы
3,252525...= 3+0,25+0,0025+0,000025+...
Сумма 0,25+0,0025+0,000025+... представляем сумму бесконечной геометрической прогрессии
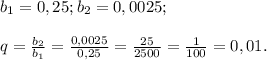
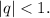
Найдем сумму бесконечно убывающей геометрической прогрессии по формуле
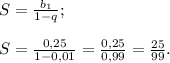
Тогда
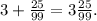
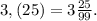
1)f(x)=
2)
возьмем производную
(-x^3-2x^2+4x+5)=-3x^2-4x+4
найдем нули производной т.е.дискриминант)
-3x^2-4x+4=0
D/4=4+12=16=4
x=2+4=-2
x=2-4=2/3
отложим корни
расставим знаки
функция убывает на [-2;2/3]
функция возростает на (-бесонечности;-2]u[2/3;+бесконечности)
3)f(x)=x^4-8x^3-10
так же возьмем производную
x^4-8x^3-10=4x^3-24x^2
4x^3-24x^2=0
4x^2(x-6)=0
x=0 x=6
отложим корни
расставим знаки
функция убывает на (-бесконечности;6]
функция возростает на [6;+бесконечности)
4)f(x)=(x^2+2x)/(4x-1)
производная
(x^2+2x)/(4x-1)=((2x+2)(4x-1)-4(x^2+2x))/(4x-1)^2=(4x^2-2x-2)/(4x-1)^2=((x-1)(x+1/2))/(4x-1)^2 ООФ x не равен 1/4
нули производной
x=1
x=-1/2
отложим корни
расставим знаки
функция убывает на [-1/2;1/4)u(1/4;1]
функция возростает на (-бесконечности; -1/2]u[1;+бесконечности)