Объяснение:
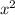 +6х-6х-36-8=
+6х-6х-36-8=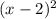 -х
-х
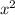 -44=
-44=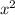 -4х+4-х
-4х+4-х
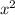 -44-
-44-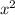 +4х-4-х=0
+4х-4-х=0
-48+3х=0
3х=48
х=16
1. Докажите тождество
sin3α +sin6α +sin7α +sin10α =4sin6,5αcos2αcos1,5α
2. Докажите тождество sin3α = 3sinα - 4sin³α
1. * * * sinα + sinβ = 2sin(α+β)/2 * cos(α+β)/2 ; cos(- φ) = cosφ * * *
Группировать можно по разному :
(sin6α +sin3α) + (sin10α+ sin7α) = 2sin4,5α*cos1,5α +2sin8,5α*cos1,5α =
2cos1,5α(sin8,5α +sin4,5α) = 4cos1,5α*sin6,5α*cos2α . - - - - - - - - - - - - - -
(sin10α+sin6α ) +(sin7α + sin3α) =2sin8α*cos2α+2sin5α*cos2α =
2(sin8α + sin5α)cos2α = 4sin6,5*α*cos2α *cos1,5α . - - - - - - - - - - - - - -
( sin7α +sin6α) + (sin10α +sin3α) = 2sin6,5α*cos0,5α +2sin6,5α*cos3,5α =
2sin6,5α(cos3,5α+cos0,5α) = 4sin6,5α*cos2α*cos1,5α .
- - - - - - - - - - - - - - - - - - - - -
2. * * * sin(α+β) =sinα*cosβ+ sinβ*cosα || β=α|| ⇒ sin2α =2sinα*cosα ;
cos(α+β) =cosα*cosβ- sinα*cosβ || β=α|| cos2α=cos²α -sin²α =1 -2sin²α * *
- - - - - - - - - - - - - - sin3α = sin(2α +α) = sin2α*cosα+*sinα*cos2α =
2sinα*cos²α +(1 -2sin²α)*sinα =sinα*(2cos²α + 1 - 2sin²α ) =
sinα*(2(1 - sin²α) + 1 - 2sin²α ) = sinα*(3 - 4sin²α) =3sinα - 4sin³α .
- - - - - - - - - - - - - -
P.S. sin3α +sin6α =2sin4,5α*cos( -1,5α) = 2sin4,5α*cos1,5α
у(x) =cosx →четная функция у(-x) = cos(-x) = cosx =y(x)
(x-6)(x+6)+8 = (x-2)²
x²-36+8 = x²-4x+4
-36+8 =-4x+4
-28 = -4x+4
4x = 4+28
4x = 32
x = 8
Объяснение: