Формула решения квадратного уравнения!
ax^2+bx+c=0
x1=(-b+кор.кв.( b^2-4ac))/2a
x2=(-b-кор.кв.( b^2-4ac))/2a
где:
^2- значит в квадрате!
кор.кв.( b^2-4ac) - корень квадратный из выражения (b в квадрате -4*a*c)
1)5x^2-7x+2=0
x1=(7+кор.кв(49-40))/10=(7+3)/10= 1
х2=(7-кор.кв(49-40))/10=(7-3)/10= 0,4
2)3x^2+5x-2=0
x1=(-5+кор.кв.(25-24))/6=(-5+1)/6=-4/6= -2/3
x2=(-5-кор.кв.(25-24))/6=(-5-1)/6=-6/6= -1
3)2x^2-7x+3=0
x1=(7+кор.кв.(49-24))/4=(7+5)/4=12/4= 3
x2=(7-кор.кв.(49-24))/4=(7-5)/4=2/4= 1/2
4)3x^2+2x-5=0
x1=(-2+кор.кв(4+60))/6=(-2+8)/6= 1
x2=(-2-кор.кв(4+60))/6=(-2-8)/6=-10/6= -1(2/3)
5)5x^2-3x-2=0
x1=(3+кор.кв.(9+40))/10=(3+7)/10=10/10= 1
x2=(3-кор.кв.(9+40))/10=(3-7)/10=-4/10= -0,4
2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
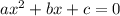
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
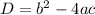
Формула корней:
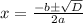
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
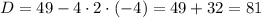
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
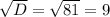
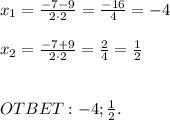
б) (4ac-2axy-9x-3ay):3a